Nagarjun sagar dam is filled water till a height of 127 metres. If the mass of water per cubic centimeter is one gram, then find the difference in pressures acting at the following two points.
(i) Point exactly at a depth half that of the dam.
(ii) Point at the bottom of the dam.
Height/depth of dam = 127 metres.
Density (d)== 1000 kg
Height of the point =
Pressure at a point =hdg
pascals
Similar Questions
Nagarjun sagar dam is filled water till a height of 127 metres. If the mass of water per cubic centimeter is one gram, then find the difference in pressures acting at the following two points.
(i) Point exactly at a depth half that of the dam.
(ii) Point at the bottom of the dam.
View SolutionNagarjun sagar dam is filled water till a height of 127 metres. If the mass of water per cubic centimeter is one gram, then find the difference in pressures acting at the following two points.
(i) Point exactly at a depth half that of the dam.
(ii) Point at the bottom of the dam.
View Solution
Knowledge Check
The figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)

Equation for the flow rate, i.e. the mass of water flowing through a given point in the stream per unit time, as funcation of the water speed v will beAvρwπD2/4Bvρw(πD2/4−πD20/4)CvρwπD22DvρwπD02/4The beaver had made a dam about hundred yards long, and it had formed out of the quickly flowing stream, a wide stretch of water about twelve feet deep. The dam was so firm and broad that it was easy for me to walk along it. After a hundred and fifty yards I came to a .beaver.s castle. - a great heap of logs skilfully fitted together, the lower part covered with earth and plants. The upper logs were put loosely together so that the air could pass through to the interior.
In the late autumn, before land and water are covered with snow and ice, the beaver has to make its dwelling frost-proof. It collects young trees and gnaws the stems in a double cone until the tree falls. Then the long stems are gnawed into small sections, the thin twigs bitten off and the logs are dragged to the dwelling. There, the timber is piled on the castle, sometimes to a height of ten or twelve feet. Mud is brought up from the bottom of the lake and packed between the logs with the animal.s clever forepaws. The interior is lined with the finest wood shavings. In this tall shelter, the beaver remains high and dry, and protected from frost throughout the winter.
The only access to the dwelling is under the water, and even the forest wolves are not able to pull the firm building apart. The water is the beaver.s element. On land it moves slowly and awkwardly. Thus, it is vital for the beaver to have water in which it can swim, and where nature has not provided this condition for it, it creates it with its dam.
The beaver.s activities can change whole landscapes. With this dam, for instance, on which I was standing, beavers had turned a whole wooded alley into a lake, trees that stood there had been killed by the water and had disappeared. Aquatic game had settled there. Ducks swam past us, and great must have been the number of fish, as swarms of trout had swum past me in the clear stream. Wide stretches of meadow had come into existence on the banks, with flat landing places to which the well-beaten beaver tracks led. Many years of building, gnawing and dragging must have gone into the completion of this immense task, creating a new region for the beaver to live in.
Which of the following statements is NOT true?AThe beaver has to make its dwelling frost-proof before it starts snowing.BThe beaver can move quickly and easily on land and in water.CThe access to the beaver.s dwelling is under the water.DWide stretches of meadows may come into existence on the banks of streams.Water is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:Ax increases with time.Bx decreases with time.CAs long as water comes out of hole, the time taken by a water particle starting from hole to reach the horizontal surface remians constant.DAs long as water comes out of hole, the time taken by a water particle starting from hole to reach the horizontal surface decreases
A dam is filled water till a height of 130m.If the mass of water per cubic centimeter is 1g,then find the pressure acting at bottom of dam A) 130×105Pa B) 13×105Pa C) 130Pa D) 13Pa
View Solution
Water is filled in a capillary tube of radius R. If the surface of water is hemispherical (θ=0), then find pressure at a point 'A' which is at h depth below the surface.
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View Solution(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
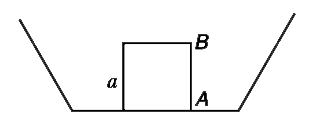
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
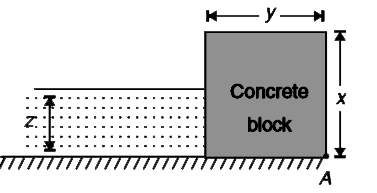
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
View SolutionA conical vessel whose height is 4 metres and of base radius 2 metres is being filled with water at the rate of 0.75 cubic metres per minute. Find the rate at which the level of the water is rising when the depth of water is 1.5 metres.?
View Solution
