Question

गोलीय अवतल दर्पण की वक्रता त्रिज्या (R) एवं फोकस दूरी (f) में संबंध स्थापित कीजिए।

Explanation

अवतल दर्पण के लिये-

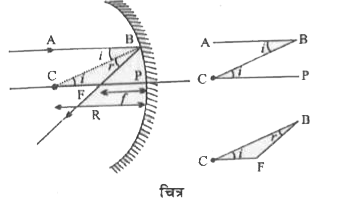
चित्रानुसार एक अवतल दर्पण लेते हैं जिसका मुख्य अक्ष CP, ध्रुव P, फोकस दूरी f तथा वक्रता केन्द्र C है। मुख्य अक्ष के समांतर आने वाली प्रकाश किरण AB अवतल दर्पण से परावर्तित होकर फोकस F से होकर जाती है। अत: यह CB गोलीय दर्पण की परिधि के बिन्दु B पर खींची जाने वाली स्पर्श रेखा पर लंब होगी।
अत: `/_ ABC =/_ CBF` (परावर्तन के नियम से) ...(1)
चूँकि AB मुख्य अक्ष (CP) के समांतर (`AB|\|CP`) है। और BC उन्हें काटती है।
अतः `/_ ABC =/_ BCF` (एकान्तर कोण बराबर) ...(2)
अब `Delta` CBF में,
समी. (1) व (2) से
`/_ BCF=/_ CBF`
अतः CF = BF (समान कोण के सामने की भुजा बराबर होती है)`" "`...(3)
यदि बिन्दु B दर्पण के ध्रुव P के अत्यंत समीप हो और दर्पण की वक्रता कम हो तो,
BF = PF`" "`...(4)
अत: समी. (3) व (4) से
CF = PF`" "`...(5)
अब CP =CF+ PF
परन्तु समी. (5) से,
CP = PF+ PF
`implies` CP=2PF
`implies PF = (CP)/(2)`
अर्थात् फोकस दूरी (f)=`1/2 xx" वक्रता त्रिज्या"`
अतः अतः किसी गोलीय (अवतल) दर्पण की फोकस दूरी, उसकी वक्रता त्रिज्या की आधी होती है।
नोट-यह संबंध उत्तल दर्पण के लिये भी सत्य है।