Write the rate law and order for the following reaction:
AB2+C2→AB2C+C (slow)
AB2+C→AB2C( fast)
To determine the rate law and order of the given reaction, we will analyze the provided steps of the reaction.
Step 1: Identify the Slow Step
The reaction consists of two steps:
1. AB2+C2→AB2C+C (slow)
2. AB2+C→AB2C (fast)
The slow step is the rate-determining step. Therefore, the rate law will be based on this step.
Step 2: Write the Rate Law from the Slow Step
The rate law can be expressed using the concentrations of the reactants involved in the rate-determining step. For the slow step:
- The reactants are AB2 and C2.
The rate law is given by:
Rate=k(AB2)m(C2)n
where m and n are the stoichiometric coefficients of the reactants in the slow step.
From the slow step, we see:
- The coefficient of AB2 is 1.
- The coefficient of C2 is 1.
Thus, the rate law becomes:
Rate=k(AB2)1(C2)1
or simply:
Rate=k(AB2)(C2)
Step 3: Determine the Order of the Reaction
The order of the reaction is the sum of the powers of the concentration terms in the rate law.
From the rate law:
- The power of (AB2) is 1.
- The power of (C2) is 1.
Therefore, the overall order of the reaction is:
Order=1+1=2
Final Answer
- Rate Law: Rate=k(AB2)(C2)
- Order of the Reaction: 2
---
The reaction consists of two steps:
1. AB2+C2→AB2C+C (slow)
2. AB2+C→AB2C (fast)
The rate law can be expressed using the concentrations of the reactants involved in the rate-determining step. For the slow step:
- The reactants are AB2 and C2.
Rate=k(AB2)m(C2)n
where m and n are the stoichiometric coefficients of the reactants in the slow step.
- The coefficient of AB2 is 1.
- The coefficient of C2 is 1.
Rate=k(AB2)1(C2)1
or simply:
Rate=k(AB2)(C2)
The order of the reaction is the sum of the powers of the concentration terms in the rate law.
- The power of (AB2) is 1.
- The power of (C2) is 1.
Order=1+1=2
- Rate Law: Rate=k(AB2)(C2)
- Order of the Reaction: 2
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - EXERCISE (PART- II (DESCRIPTIVE QUESRTIONS) B. SHORT ANSWER QUESTIONS )
119 Videos
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - EXERCISE (PART- II (DESCRIPTIVE QUESRTIONS) C.LONG ANSWER QUESTIONS )
54 Videos
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - EXERCISE (PART- I (OBJECTIVE QUESRTIONS) D. MATCH THE FOLLOWING )
3 Videos
- BIOMOLECULESBOOK - ICSECHAPTER - BIOMOLECULESEXERCISE - ISC EXAMINATION QUSTIONS (PART-I)(DESCRIPTIVE QUESTIONS)
21 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - ICSECHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - EXERCISE (PART - II (DESCRIPTIVE QUESTIONS) (LONG ANSWER QUESTIONS))
19 Videos
Similar Questions
Knowledge Check
The reaction ,2AB(g)+2C(g)→A2(g)+2BC(g) proceeds according to the mechanism .
I. 2AB⇔A2B2 (fast)
II. A2B2+C→A2B+BC (slow )
III. A2B+C→A2+BC (fast)
what will be the initial rate taking [AB] = 0.2 M and [C] = 0.5 M ? The Kc for the step I is 102M−1 and rate constant for the step II is 3.0×10−3mol−1−1minA0.0716M−1minB0.0891M−1minC0.006M−1minD0.0257M−1minA hypothetical reaction A2+B2→2AB follows the mechanism as given below:
A2⇔A+A(fast)
A+B2→AB+B (slow)
A+B→AB (fast)
The order of the overall reaction isA2B1C1.5DzeroIf A and Bare square matrices of same order such that AB = A and BA = B, then AB2+B2=:
AABBA+BC2ABD2BA
State with reason, whether the following are true of false. A, B and C are matrices of order 2×2.
A.(B-C)=A.B-A.C
View SolutionState with reason, whether the following are true or false, A,B, and C are matrices of order 2×2
(i) A.B=B.A (ii) A. (B.C)=(A.B).C
(iii) (A+B)2=A2+2AB+B2 (iv) A.(B+C)=A.B+A.C
View SolutionThe C.N.of A2+ in AB2 is 8, then C.N. of B is
View Solutionin figure, ABC is an isosceles traingle, right angled at C. therefore
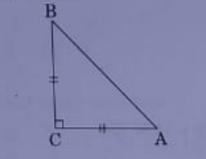
a) AB2=2AC2
b) BC2=2AB2
c) AC2=2AB2
d) AB2=4AC2
View SolutionFactorise a2−2ab+b2−c2
View Solution
