The rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R = 8.314 JK−1mol−1)
The correct Answer is:55.33KJmol−1
To solve the problem of calculating the energy of activation (Ea) for a reaction that increases its rate four times when the temperature changes from 300 K to 320 K, we can use the Arrhenius equation in its logarithmic form. Here are the steps to arrive at the solution:
Step 1: Understand the relationship between rate constants and temperature
Given that the rate of the reaction increases four times when the temperature changes, we can express this as:
k2=4k1
where k1 is the rate constant at 300 K and k2 is the rate constant at 320 K.
Step 2: Use the Arrhenius equation
The Arrhenius equation in logarithmic form is given by:
ln(k2k1)=EaR(1T1−1T2)
where:
- Ea is the activation energy,
- R is the universal gas constant (8.314 J K−1 mol−1),
- T1 is the initial temperature (300 K),
- T2 is the final temperature (320 K).
Step 3: Substitute values into the equation
Since we know that k2=4k1, we can write:
ln(4)=EaR(1300−1320)
Step 4: Calculate ln(4)
We know:
ln(4)≈1.386
Step 5: Calculate the temperature difference
Now calculate 1300−1320:
1300−1320=320−300300×320=2096000=14800
Step 6: Substitute into the equation
Now substituting back into the equation:
1.386=Ea8.314(14800)
Step 7: Rearranging to find Ea
Rearranging gives:
Ea=1.386×8.314×4800
Step 8: Calculate Ea
Now perform the calculation:
Ea=1.386×8.314×4800≈55,327.2 J/mol
Final Answer
Thus, the energy of activation Ea is approximately:
Ea≈55,327.2 J/mol
---
Given that the rate of the reaction increases four times when the temperature changes, we can express this as:
k2=4k1
where k1 is the rate constant at 300 K and k2 is the rate constant at 320 K.
The Arrhenius equation in logarithmic form is given by:
ln(k2k1)=EaR(1T1−1T2)
where:
- Ea is the activation energy,
- R is the universal gas constant (8.314 J K−1 mol−1),
- T1 is the initial temperature (300 K),
- T2 is the final temperature (320 K).
Since we know that k2=4k1, we can write:
ln(4)=EaR(1300−1320)
We know:
ln(4)≈1.386
Now calculate 1300−1320:
1300−1320=320−300300×320=2096000=14800
Now substituting back into the equation:
1.386=Ea8.314(14800)
Rearranging gives:
Ea=1.386×8.314×4800
Now perform the calculation:
Ea=1.386×8.314×4800≈55,327.2 J/mol
Thus, the energy of activation Ea is approximately:
Ea≈55,327.2 J/mol
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - INTEXT QUESRTIONS
81 Videos
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - EXERCISE (PART- I (OBJECTIVE QUESRTIONS)A.FILL IN THE BLANKS)
54 Videos
- CHEMICAL KINETICSBOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - ISC EXAMINATION QUESTIONS (NUMERICAL PROBLEMS )
57 Videos
- BIOMOLECULESBOOK - ICSECHAPTER - BIOMOLECULESEXERCISE - ISC EXAMINATION QUSTIONS (PART-I)(DESCRIPTIVE QUESTIONS)
21 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - ICSECHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - EXERCISE (PART - II (DESCRIPTIVE QUESTIONS) (LONG ANSWER QUESTIONS))
19 Videos
Similar Questions
The rate of a reaction quadruples when the temperature changes from 293K to 313K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
View SolutionThe rate of a reaction triples when temperature changes from 20∘C to 50∘C. Calculate the energy of activation.
View SolutionThe rate of reaction triples when temperature changes form 20∘C to 50∘C. Calculate the energy of activation for the reaction (R=8.314JK−1mol−1).
View SolutionThe rates of most reaction double when their temperature is raised from 298K to 308K. Calculate their activation energy.
View SolutionThe rate of a reaction becomes 4 times when temperature is raised from 293 K to 313 K. The activation energy for such reaction would be
View SolutionThe rate of a reaction triples when temperature changes from 50∘ C to 100∘C. Calculate the energy of activation for such a reaction. (R=8.314JK−1mol−1log3=0.4771)
View SolutionThe rate of a reaction triples when temperature changes from 50∘ C to 100∘C. Calculate the energy of activation for such a reaction. (R=8.314JK−1mol−1log3=0.4771)
View SolutionThe rate of a reaction triples when temperature changes from 50∘ C to 100∘C. Calculate the energy of activation for such a reaction. (R=8.314JK−1mol−1log3=0.4771)
View SolutionThe rate of a reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If K is the rate constant at 310 K will be equal to
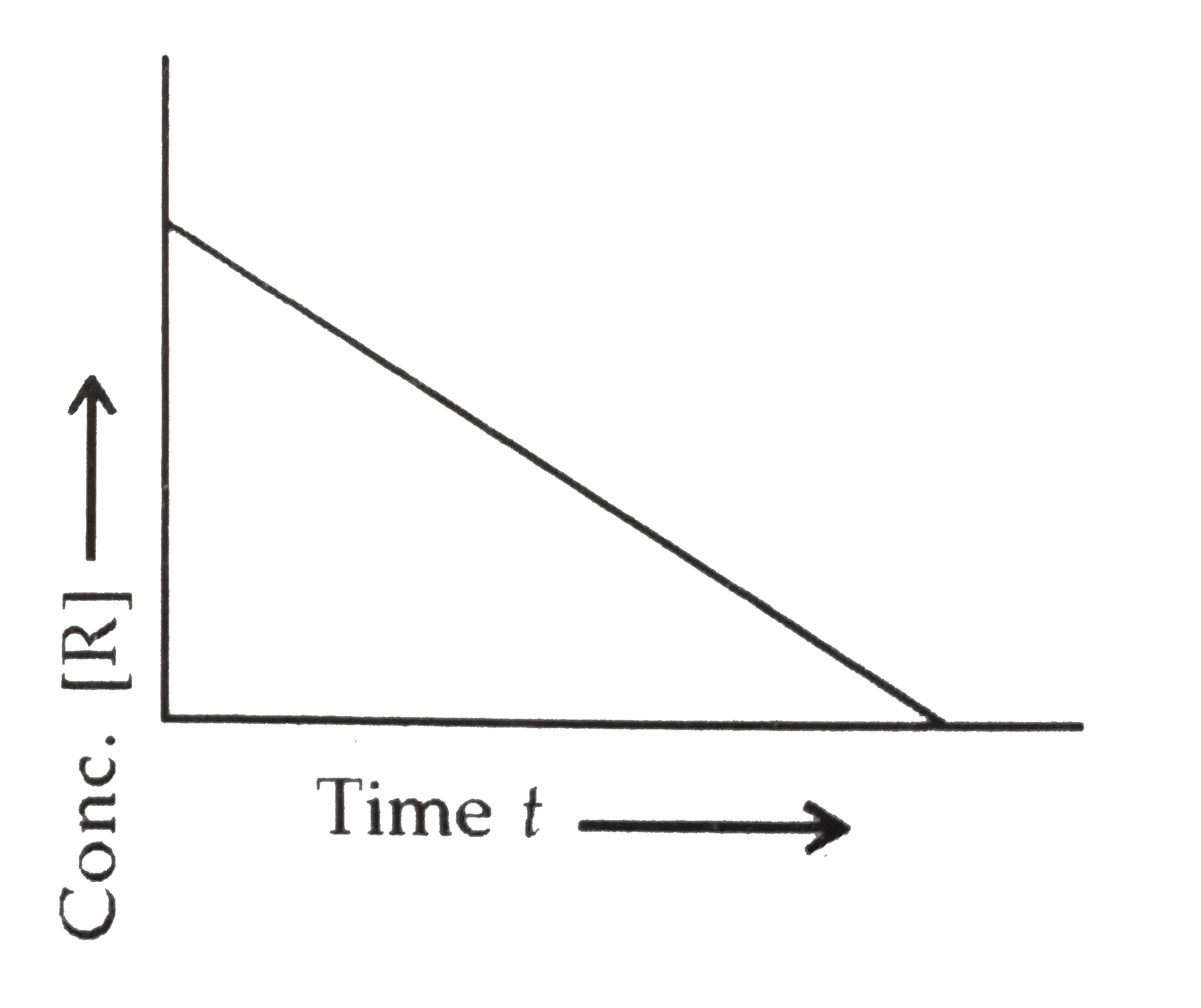
View SolutionConsider the reaction R→P for which the change in concentration of R with time is shown by the following graph:
( i) Predict the order of reaction .
( iii) What does the slope of the curve indicate ?
( b) The rate of reaction quadruples when temperature chages from 293 K of 313 K .Calculate Ea assuming that it does not chage with time [R=8.314JK−1mol−1]
View Solution
