For of particles under central forcer field, the total angular momentum is conserved.
The torque acting on such a system is zero.
If both assertion and reason are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion
If assertion is true but reason is false
If both assertion and reason are false
The correct Answer is:A
To solve the question regarding the conservation of angular momentum for a particle under a central force field, we will analyze the assertion and the reason provided in the statement.
1. Understanding Central Force:
A central force is a force that acts along the line connecting the particle and a fixed point (the center). Examples include gravitational and electrostatic forces.
2. Torque in Central Force Fields:
The torque (τ) acting on a particle due to a central force is given by the equation:
τ=→r×→F
where →r is the position vector from the center to the particle and →F is the force vector. For a central force, →F is directed along →r, making the angle between →r and →F equal to 0 degrees.
3. Calculating Torque:
Since the angle between →r and →F is 0 degrees, the sine of the angle is zero:
τ=rFsin(0)=0
Therefore, the torque acting on the system is zero.
4. Conservation of Angular Momentum:
The angular momentum (→L) of a particle is defined as:
→L=→r×→p
where →p is the linear momentum. The rate of change of angular momentum is equal to the torque:
d→Ldt=τ
Since we have established that τ=0, it follows that:
d→Ldt=0⟹→L=constant
This indicates that angular momentum is conserved.
5. Conclusion:
Both the assertion that "the total angular momentum is conserved" and the reason that "the torque acting on such a system is zero" are true. Moreover, the reason correctly explains the assertion.
Final Answer:
The correct option is a: Both assertion and reason are true, and the reason is the correct explanation of the assertion.
A central force is a force that acts along the line connecting the particle and a fixed point (the center). Examples include gravitational and electrostatic forces.
The torque (τ) acting on a particle due to a central force is given by the equation:
τ=→r×→F
where →r is the position vector from the center to the particle and →F is the force vector. For a central force, →F is directed along →r, making the angle between →r and →F equal to 0 degrees.
Since the angle between →r and →F is 0 degrees, the sine of the angle is zero:
τ=rFsin(0)=0
Therefore, the torque acting on the system is zero.
The angular momentum (→L) of a particle is defined as:
→L=→r×→p
where →p is the linear momentum. The rate of change of angular momentum is equal to the torque:
d→Ldt=τ
Since we have established that τ=0, it follows that:
d→Ldt=0⟹→L=constant
This indicates that angular momentum is conserved.
Both the assertion that "the total angular momentum is conserved" and the reason that "the torque acting on such a system is zero" are true. Moreover, the reason correctly explains the assertion.
The correct option is a: Both assertion and reason are true, and the reason is the correct explanation of the assertion.
Similar Questions
Knowledge Check
Assertion: The motion of a particle under the central force is always confined to a plane.
Reason: Angular momentum is always conserved in the motion under a central force.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are truebut reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false.Total angular momentum of a rotating body remains constant, if the net torque acting on the body is
AzeroBmaximumCminimumDunity
Two particle A and B are moving as shown in the figure
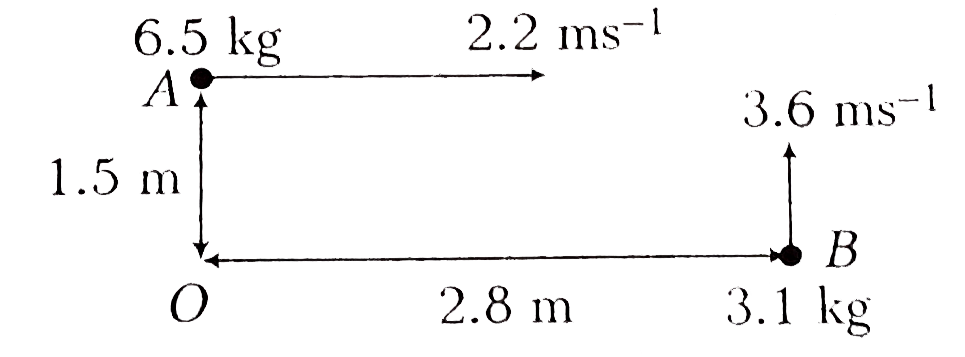
Their total angular momentum about the point O is
View SolutionRelation between torque and angular momentum is similar to the relation between
View SolutionThe conservation of angular momentum demands that
View SolutionA coil of radius R carries a current i1. Another concentric coil of radius r(r<<R) carries a current i2. Planes of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. Find maximum kinetic energy attained by the two coils, when both are released from rest. The masses of two coils are M and m respectively.
Strategy : The magnetic field due to coil of radius R is μ0i12R. This field exerts a torque on shorter coil. An equal and opposite torque is exerted by the shorter coil on larger coil. There is no external torque acting on the system. The angular momentum remains conserved. Also the total mechanical energy remains conserved. At any instant, let ω1andω2 represent the angular velocity
View SolutionWrite down the relation connecting torque and angular momentum ?
View SolutionThe angular momentum of a system of particles is conserved
View Solution

