x-y relation is given by y=xn calculate the value of n in the following :-
(i)y=x2x2/3
(ii)y=x3/2x1
(iii)y=x1/2x1/2
(iv)y=x3/2√xSolution in Gujrati
The correct Answer is:(i)43
(ii)12
(iii) 1
(iv) 1
Step by step video & image solution for x-y relation is given by y=x^(n) calculate the value of n in the following :- (i)y=(x^(2))/(x^(2//3)) (ii)y=(x^(3//2))/(x^(1)) (iii)y=(x^(1//2))/(x^(1//2)) (iv)y=(x^(3//2))/(sqrt(x)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBook:ALLEN Chapter:RACEExercise:Basic Maths (VECTORS)
Explore 62 Videos
- RACEBook:ALLEN Chapter:RACEExercise:Basic Maths (Units, Dimensions & Measurements)
Explore 37 Videos
- RACEBook:ALLEN Chapter:RACEExercise:Basic Maths (Graphs))
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLEN Chapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLEN Chapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
State whether the following relations are true or false
(1)−−→AB=−−→BA
(2)−−→AB=−−−→BA
(3)∣∣∣−−→AB∣∣∣=∣∣∣−−→BA∣∣∣
(4)∣∣∣−−→AB∣∣∣=∣∣∣−−−→AB∣∣∣
(5)ˆj=ˆk
(6)∣∣ˆj∣∣=∣∣ˆk∣∣
View SolutionWhich one of the following is not a fundamental quantity ?
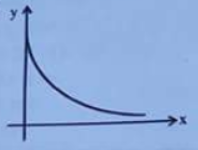
View SolutionWhich of the following equation is best representation of following graph's?
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionIf sin^(-1)((x^2-y^2)/(x^2+y^2)) = tan^(-1)a, then the value of dy/dx is (i)x/y (ii)-x/y (iii)y/x (iv) -y/x
View SolutionIf graph of y=(x−1)(x−2) is

then draw the graph of the following
(i)y=|(x−1)(x−2)| (ii)|y|=(x−1)(x−2)
(iii)y=(|x|−1)(|x|−2) (iv)|(|x|−1)(|x|−2)|
(v)|y|=|(|x|−1)(|x|−2)|
View Solution(x+2)(x+1)=(x−2)(x−3)
(y+3)(y+2)=(y−1)(y−2)
View Solutionपूर्ण (शुद्ध) करणी के रूप में लिखिएः
(i) √x+yx−y (ii) √(x3+y3)(x2−y2)
(iii) (x−y)√x+yx−y (iv) xy23√y7x2
View Solutionसरल विधि से हल कीजिए :
(i) (x+y)(x−y) (ii) (4+x)(4−x) (iii) (2x−1)(2x+1) (iv) (xy+a)(xy−a)
(v) (x2−y3)(x2+y3) (vi) (x+y)(x−y)(x2+y2)
View SolutionIf Sn=(x+y)+(x2+xy+y2)+(x3+x2y+y2x+y3)+…n terms then prove that (x−y)Sn=[x2(xn−1)x−1−y2yn−1y−1].
View SolutionSn = (x+y)+(x2+xy+y2)+(x3+x2y+xy2+y3)+.....n உறுப்புகள் வரை எனில் (x−y)Sn=[(x2(xn−1)x−1)−(y2(yn−1)y−1)] என நிறுவுக
View SolutionFind the value of (x+y), if (x+y3x2)−1−(x2y+y2x)−1+(x3y2+y)−1=13
View SolutionFind the value of (x+y) ,if (x+y3x2)−1−(x2y+y2x)−1+(x3y2+y)−1=13
View SolutionVerify : (i) x3+y3=(x+y)(x2−xy+y2) (ii) x3−y3=(x−y)(x2+xy+y2)
View SolutionIf |x|<1and|y|<1, find the sum of infinity of the following series: (x+y)+(x2+xy+y2)+(x3+x2y+xy2+y3)+
View Solution

