Supposing Newton's law of gravitational for gravitation fores →F1 and →F2 between two masses m1 and m2 at positions →r1 and →r2 read →F1=−→F2=−→r12r312GM10(m1m2m20)n where M0 is a constant of dimension of mass. →r12=→r1−→r2 and n is a number. In such a case Solution in Punjabi
the acceleration due to gravity on earth will be different for different objects.
noene of three laws of Kepler will be valid.
only the thrid law will become invalid.
for n negative, an object lighter than water will sink in water.
Step by step video & image solution for Supposing Newton's law of gravitational for gravitation fores vecF_1 and vecF_2 between two masses m_1 and m_2 at positions vecr_1 and vecr_2 read vecF_1 = - vecF_2 = - (vecr_12)/(r_12^3) GM_0^1((m_1m_2)/(m_0^2))^n where M_0 is a constant of dimension of mass. vecr_12 = vecr_1 - vecr_2 and n is a number. In such a case by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What is the difference between gravity and gravitation?
View SolutionA gas enclosed in a container is heated up What is the effect on pressure?
View SolutionHow is inertia related to mass of a body?
View SolutionTwo constant forces →F1 and →F2 act on a body of mass 8kg. These forces displace the body from point P(1,−2,3) to Q (2,3,7) in 2s starting from rest. Force →F1 is of magnitude 9N and is acting along vector (2ˆi−2ˆj+ˆk). Work done by the force →F2 is
View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
View SolutionSupposing Newton's law of gravitation for gravitation forces F_(1) and F_(2) between two masses m_(1) and m_(2) at positions r_(1) and r_(2) read where M_(0) is a constant of dimension of mass, r_(12) = r_(1) - r_(2) and n is a number. In such a case,
View SolutionGiven three non-zero, non-coplanar vectors →a,→band→c. →r1=p→a+q→b+→cand→r2=→a+p→b+q→c. If the vectors →r1+2→r2and2→r1+→r2 are collinear, then (p,q) is
View Solutionएक कण स्थिति →r1 से स्थित →r2 तक गति करता है कण का विस्थापन कितना है
View Solutionसमतल में गतिमान कण का प्रारम्भ में स्थिति सदिश →r1=−3ˆi+2ˆj तथा कुछ समय बाद स्थिति सदिश →r2=9ˆi+2ˆj है →r1 से →r2 तक कण का विस्थापन ज्ञात कीजिय
View SolutionAt what angle the two forces (→F1+→F2)and(→F1−→F2) act so that the resultant is of magnitude √2(F21+F22)
View Solutionएक कण पर दो बल →F1और →F2 लग रहे हैं और कण नियत वेग →v=3ˆi−4ˆj (मी./से.) से गतिशील रहता है। यदि →F1=2ˆi+3ˆj न्यूटन हो तब दूसरे बल →F2 का मान क्या है?
View Solutionमाना →r1(t)=3tˆi+4t2ˆj और →r2(t)=4t2ˆi+3tˆj क्रमशः वस्तु 1 तथा 2 की स्थिति, समय के सापेक्ष प्रदर्शित करते हैं। →r1(t) और →r2(t) मीटर में तथा t सेकण्ड में है। तब क्षण t=1s, पर दो वस्तुओं की आपेक्षिक गति होगी
View SolutionSupposing Newton's Law of gravitation for gravitation forces F1andF2 between two masses my and m, at positions r1andr2 read F1=−F2=−r12r123GM20(m1m2M20)2
where M0 is a constant of dimension of mass,r12=r1−r2 and n is a number. In such a case,
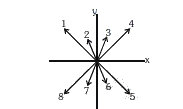
View Solutionदो बल →F1=(3N)ˆi−(4N)ˆj व →F2=−(1N)ˆi−(2N)ˆj एक बिन्दु वस्तु पर कार्यरत है। दिये गये चित्र में आठ सदिशों में से कौन से सदिश →F1 व →F2 को प्रदर्शित करते हैं तथा कुल बल का परिमाण क्या होगा?
View SolutionSupposing Newton's law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read
where M0 is a constant of dimension of mass, r12=r1−r2 and n is a number. In such a case,
View SolutionGiven three non-zero, non-coplanar vectors →a,→band→c. →r1=p→a+q→b+→cand→r2=→a+p→b+q→c. If the vectors →r1+2→r2and2→r1+→r2 are collinear, then (p,q) is
View Solution
