20 किग्रा द्रव्यमान तथा 20 सेमी त्रिज्या की चकती के रिम के चारों ओर नगण्य द्रव्यमान की रस्सी लटकाई गई है। चित्र में दिखाए अनुसार 25 न्यूटन का स्थिर खिंचाव रस्सी पर लगाया गया है। चकती को विशेष दिशा में धुरी (क्षतिज) के साथ घर्षणरहित बियरिंग लगाए हैं।
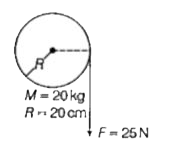
इस बिन्दु पर चकती की गतिज ऊर्जा क्या होगी? जब 2 मी रस्सी बिना बँधी हुई है। यह मानते हुए कि चकती विरामावस्था से शुरू करें।
10 जूल
30 जूल
50 जूल
20 जूल
The correct Answer is:C
माना ω अन्तिम कोणीय संवेग है
प्राप्त गतिज ऊर्जा =12Iω2
चूंकि, चकती विरामावस्था से प्रारम्भ होती है।
अब, ω2=ω20θ,ω0=0
α=12.50सेकण्ड−2
कोणीय विस्थापन
θ= बिना बँधी रस्सी की लम्बाई/चकती की त्रिज्या।
⇒θ=20.210 रेडियन
ω2=2×12.5×10.0=250(10रेडियन से−1)2
∴ प्राप्त गतिज ऊर्जा =12×0.4×250
=50 जूल ( ∴=0.4किग्रा-मी−2)
Similar Questions
fcc में कॉपर 361 pm की इकाई सेल लंबाई के साथ क्रिस्टलीकृत होता है। कॉपर परमाणु की त्रिज्या क्या है?
View Solutionसल्फर के एक यौगिक में द्रव्यमान द्वारा 8% सल्फर उपस्थित होता है। यौगिक के न्यूनतम आण्विक द्रव्यमान की गणना कीजिए।
View Solutionनिर्जल AlCl3 की उपस्थिति में क्लोरोमेथेन के साथ अभिक्रिया करने पर ऐनिसोल क्या उत्पादित करता है?
View Solutionजब प्लास्टर ऑफ पेरिस, जल के संपर्क में आता है तो यह एक कठोर द्रव्यमान में बदल जाता है। कठोर द्रव्यमान का संघटन है:
View Solutionजब आवेश, e और द्रव्यमान, m का एक इलेक्ट्रॉन, नाभिकीय आवेश 'Ze' के चारों ओर v वेग के साथ गति करता है, जो वृत्ताकार कक्षा का वर्णन करता है, तो इलेक्ट्रॉन की स्थितिज ऊर्जा है:
View Solutionबेन्जैल्डिहाइड बनाने के लिए AlCl3 की उपस्थिति में बेन्जीन के साथ CO+HCI की अभिक्रिया को क्या कहा जाता है?
View Solutionअभिक्रिया A→ उत्पाद के लिए, यह पाया गया है कि अभिक्रिया की दर 6.25 के गुणक से बढ़ जाती है, जब A की सांद्रता 2.5 के गुणक से बढ़ाई जाती है। A के संबंध में अभिक्रिया की कोटि क्या है?
View Solution0.25 मिलीमीटर मोटी क्रोमियम धातु की एक परत को CrO2−4 के विलयन से 32 m2 के कुल क्षेत्रफल के साथ स्वचालित वाहनों की रिम पर विद्युत्-लेपित किया जाना है। 60 सेकंड में रिम का वैद्युतलेपन करने के लिए विद्युत धारा की कितनी मात्रा की आवश्यकता होती है? क्रोमियम धातु का घनत्व 7.2 g/cc है।
View Solution
