Doubtnut Promotions Sticky

किसी त्रिज्या के क्षेत्र में एकसमान चुम्बकीय क्षेत्र को सीमित किया जाता है। चुम्बकीय क्षेत्र में समय के साथ bBdt की दर से । परिवर्तन होता है। लूप 1 की त्रिज्या R(R>r) है तथा यह r क्षेत्र के परिबद्ध है तथा R त्रिज्या का लूप 2 चुम्बकीय क्षेत्र के बाहर है जिसे चित्र में प्रदर्शित किया गया है, तो निम्नलिखित विद्युत वाहक बल उत्पन्न होगा
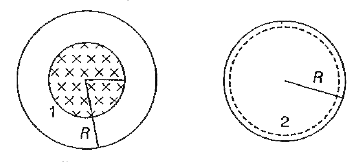
किसी त्रिज्या के क्षेत्र में एकसमान चुम्बकीय क्षेत्र को सीमित किया जाता है। चुम्बकीय क्षेत्र में समय के साथ (bB)/(dt) की दर से । परिवर्तन होता है। लूप 1 की त्रिज्या R(R gt r) है तथा यह r क्षेत्र के परिबद्ध है तथा R त्रिज्या का लूप 2 चुम्बकीय क्षेत्र के बाहर है जिसे चित्र में प्रदर्शित किया गया है, तो निम्नलिखित विद्युत वाहक बल उत्पन्न होगा

A

लूप 1 में शून्य और लूप 2 में शून्य

B

लूप 1 में −dBdtπr2 और लूप 2 में −dBdtπr2

C

लूप 1 में (−dB)πR2 और लूप 2 में शून्य

D

लूप 1 में −dBdtπr2 और लूप 2 में शून्य

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

प्रेरित विद्युत वाहक बल, |e|=dϕdt
जहाँ,ϕ=BA=πr2B
⇒dϕdt=−πr2dBdL
लूप 1 में चुम्बकीय फ्लक्स में परिवर्तन की दर e1=dϕ1dt=−πr2dBdt
e2 लूप से सम्बद्ध प्रेरित विद्युत वाहक बल
dϕ2dt=0 [∴ϕ2=0]

|
Updated on:21/07/2023
Class 12PHYSICSELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions