कोई कण इस प्रकार गमन करता है कि उसका स्थिति सदिश →r=cosωtˆx+sinωtˆy द्वारा निरूपित होता है, यहाँ ω नियतांक है | निम्न में से कौन-सा कथन सत्य है ?
वेग और त्वरण दोनों ही r के समान्तर हैं
वेग r के लम्ब्वत है तथा त्वरण मूल बिन्दु की ओर निर्देशित है
वेग r के लम्ब्वत है तथा त्वरण मूल बिन्दु से दूर की ओर निर्देशित है
वेग और त्वरण दोनों ही r के लम्ब्वत हैं
The correct Answer is:B
कण की स्थिति सदिश
r=cosωtˆx=sinωtˆy
जहाँ, ω स्थिरांक है।
कण का वेग v=drdt
=ddt(cosωtˆx+sinωtˆy)
=(−sinωt)ωˆx+(cosωt)ωˆy
=ω(sinωtˆx−cosωtˆy)
कण का त्वरण
a=dvdt=ddt[−ωsinωtˆx+ωcosωtˆy]
=−ω2cosωtˆx−ω2sinωtˆy
=−ω2(cosωtˆx+ω2sinωtˆy)
⇒a=−ω2r=ω2(−r)
मान लें कि कण P है, तब इसकी स्थिति सदिश निम्न चित्रानुसार होगी।
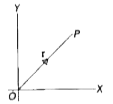 अतएव - r त्वरण की दिशा जो .O. मूलबिन्दु की ओर है।
अतएव - r त्वरण की दिशा जो .O. मूलबिन्दु की ओर है।
v⋅r=−ω(sinωtˆx−cosωtˆy)⋅(cosωtˆx+sinωtˆy)
=−ω[sinωt⋅cosωt+0+0−sinωtcosωt]
[∵ˆx⊥ˆy]
⇒ˆv⊥ˆr
इस प्रकार वेग, r पर अभिलम्बवत है।
Topper's Solved these Questions
Similar Questions
दो गुटकों A और B के द्रव्यमान, क्रमश: 3m तथा m हैं। ये आपस में एक द्रव्यमानहीन, अवितान्य डोरी से जुड़े हैं। इस पूरे निकाय को, आरेख में दर्शाए गए अनुसार एक द्रव्यमानरहित स्प्रिंग (कमानी) द्वारा लटकाया गया है। डोरी को काट देने के तुरन्त पश्चात् A और B के त्वरण के परिमाण होंगे क्रमशः
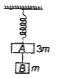 02:00View Solution
02:00View Solutionकिसी एकपरमाणुक गैस के आयतन (V) में ताप (T) के साथ विचरण ग्राफ में दर्शाए अनुसार होता है। अवस्था A से अवस्था B तक जाने की प्रक्रिया में गैस द्वारा किए गए कार्य और इसके द्वारा अवशोषित ऊष्मा का अनुपात है
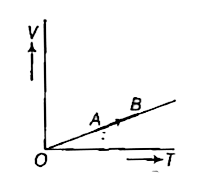 04:22View Solution
04:22View Solutionनिम्न कथन सत्य है या असत्य|
एक आव्यूह एक संख्या को निरूपित करता है ।03:23View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
03:19View Solutionसदिश →a,→b,→c एक ही समतल में हैं। निम्न में से कौन-सा असत्य है?
02:00View Solutionयदि z एक सम्मिश्र संख्या है, तो निम्न में से कौन-सा कथन सत्य है?
02:25View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"tan A का मान सदैव-1 और 1 के बीच होता है।"View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता हैView Solutionनिम्न में पत्राचार का कौन-सा प्रकार है?
View Solutionनिम्न में पत्राचार का कौन-सा प्रकार है?
View Solutionनिम्न में कौन-सा काव्य-संग्रह धूमिल द्वारा रचित है?
View Solutionनिम्नलिखित में से कौन सा कथन सत्य है?
View Solutionशून्य कोटि अभिक्रिया के बारे में निम्नलिखित में से कौन सा कथन सत्य नहीं है?
View Solutionनिम्नलिखित में से कौन सा कथन सत्य नहीं है?
View Solution[Co (CN ) _(6) ]^(3-) के बारे में निम्नलिखित में से कौन सा कथन सत्य है
View Solutionएथेन के संरूपणों के सन्दर्भ में, निम्नलिखित में से कौन सा कथन सत्य है ?
View Solution
