In an experiment of photoelectric effect the stopping potential was measured to be V1 and V2 with incident light of wavelength λ and λ2, respectively. The relation between V1 and V2 is:
V2>2V1
V2<V1
V1<V2<2V1
V2=2V1
The correct Answer is:A
To solve the problem, we need to establish the relationship between the stopping potentials V1 and V2 for the two different wavelengths of incident light in the photoelectric effect.
1. Understanding Stopping Potential:
The stopping potential V0 is related to the maximum kinetic energy of the emitted electrons. The equation for stopping potential is given by:
eV0=hcλ−ϕ
where ϕ is the work function of the metal, h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
2. Expression for V1:
For the first wavelength λ:
eV1=hcλ−ϕ
Rearranging gives:
V1=hceλ−ϕe
3. Expression for V2:
For the second wavelength λ2:
eV2=hcλ2−ϕ
This simplifies to:
eV2=2hcλ−ϕ
Rearranging gives:
V2=2hceλ−ϕe
4. Comparing V1 and V2:
Now we have:
V1=hceλ−ϕe
V2=2hceλ−ϕe
5. Finding the Relation:
To compare V1 and V2, we can multiply V1 by 2:
2V1=2(hceλ−ϕe)=2hceλ−2ϕe
6. Subtracting 2V1 from V2:
Now, we can find the difference:
V2−2V1=(2hceλ−ϕe)−(2hceλ−2ϕe)
Simplifying this gives:
V2−2V1=2ϕe−ϕe=ϕe
7. Conclusion:
Since ϕe>0, we conclude that:
V2>2V1
Final Result:
Thus, the relation between V1 and V2 is:
V2>2V1
The stopping potential V0 is related to the maximum kinetic energy of the emitted electrons. The equation for stopping potential is given by:
eV0=hcλ−ϕ
where ϕ is the work function of the metal, h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
For the first wavelength λ:
eV1=hcλ−ϕ
Rearranging gives:
V1=hceλ−ϕe
For the second wavelength λ2:
eV2=hcλ2−ϕ
This simplifies to:
eV2=2hcλ−ϕ
Rearranging gives:
V2=2hceλ−ϕe
Now we have:
V1=hceλ−ϕe
V2=2hceλ−ϕe
To compare V1 and V2, we can multiply V1 by 2:
2V1=2(hceλ−ϕe)=2hceλ−2ϕe
Now, we can find the difference:
V2−2V1=(2hceλ−ϕe)−(2hceλ−2ϕe)
Simplifying this gives:
V2−2V1=2ϕe−ϕe=ϕe
Since ϕe>0, we conclude that:
V2>2V1
Thus, the relation between V1 and V2 is:
V2>2V1
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - NEET Past 5 Years Questions
23 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - NEET PAST 5 YEARS QUESTIONS
7 Videos
Similar Questions
In photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives

View SolutionIn an experiment on photoelectric effect, a student plots stopping potential V0 against reciprocal of the wavelength λ of the incident light for two different metals A and B. These are shown in the figure

Looking at the graphs, you can most appropriately say that :
View Solution
Knowledge Check
The correct curve between the stopping potential (V) and intensity of incident light (I) is
A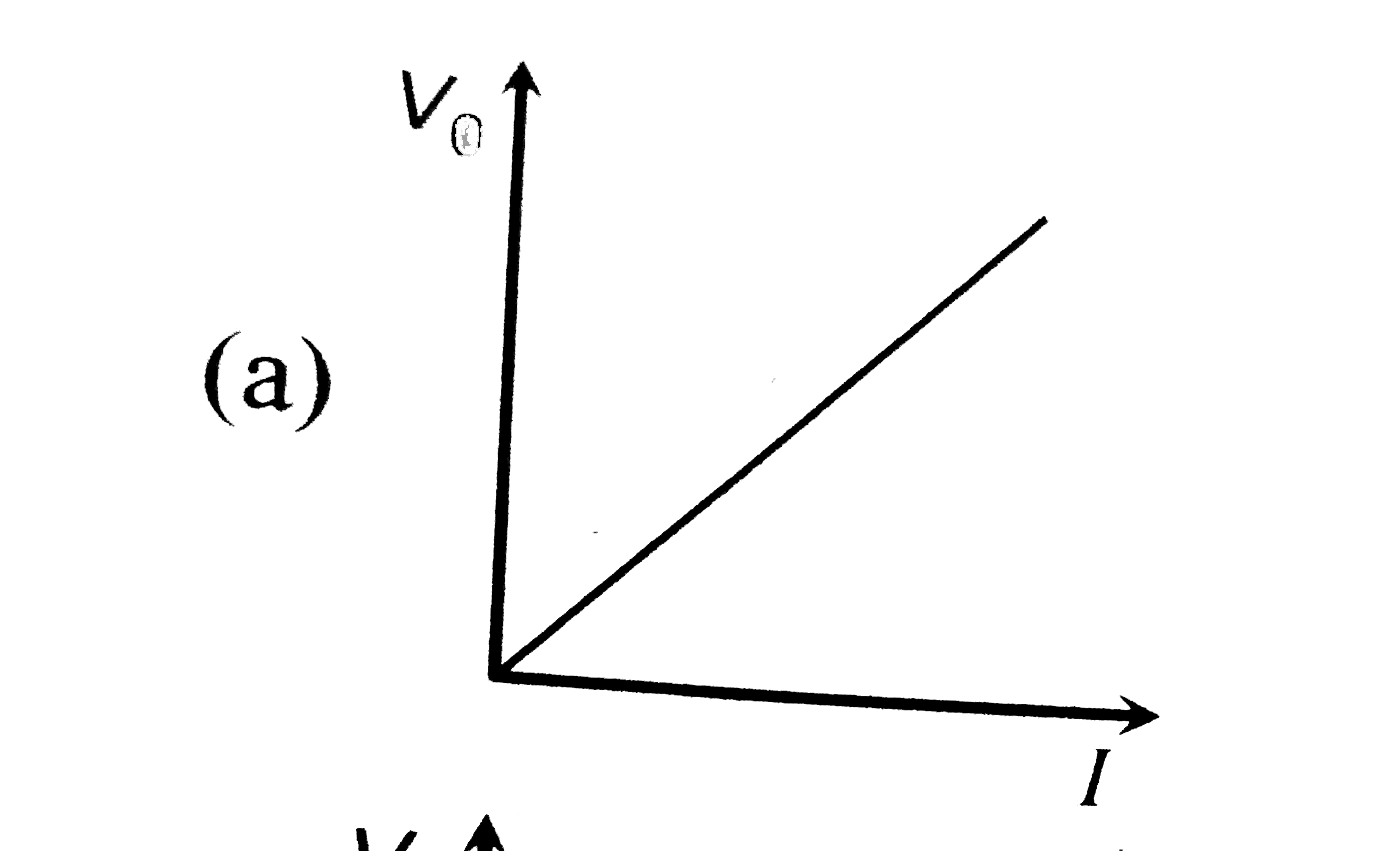 B
B C
C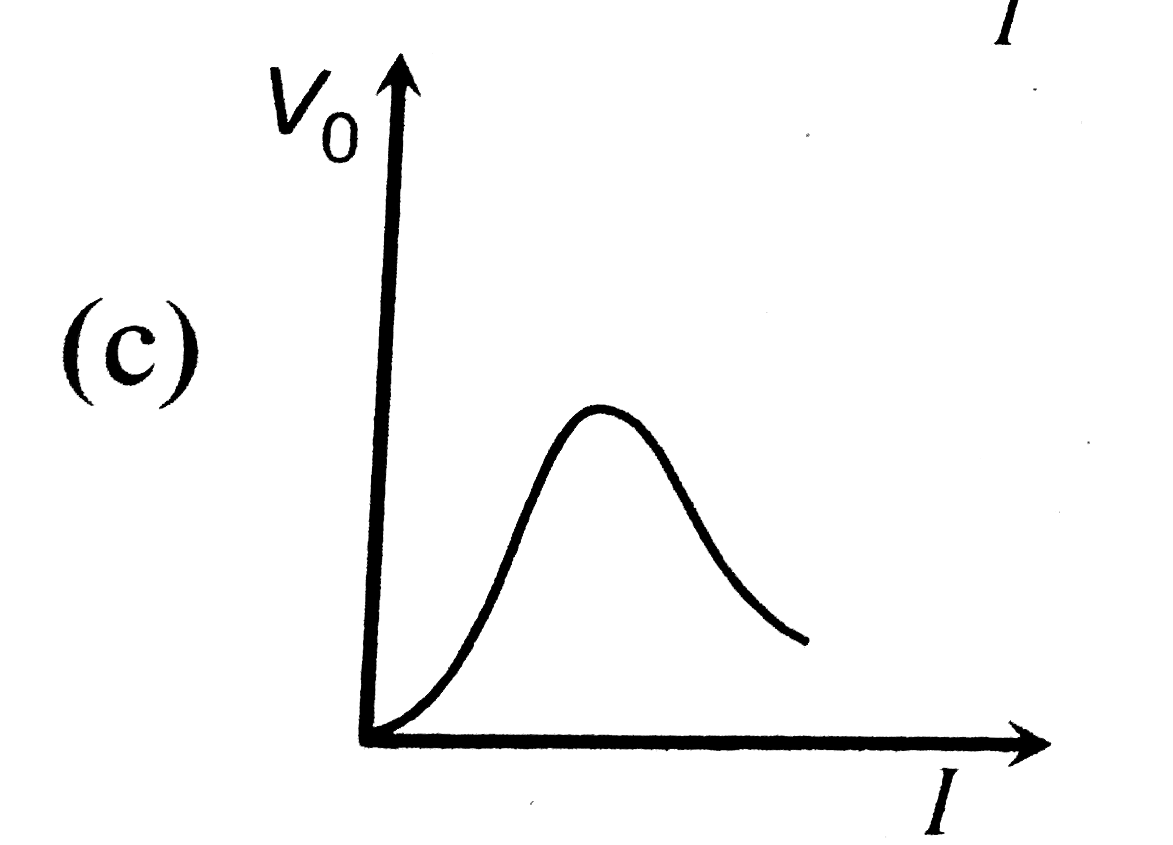 D
D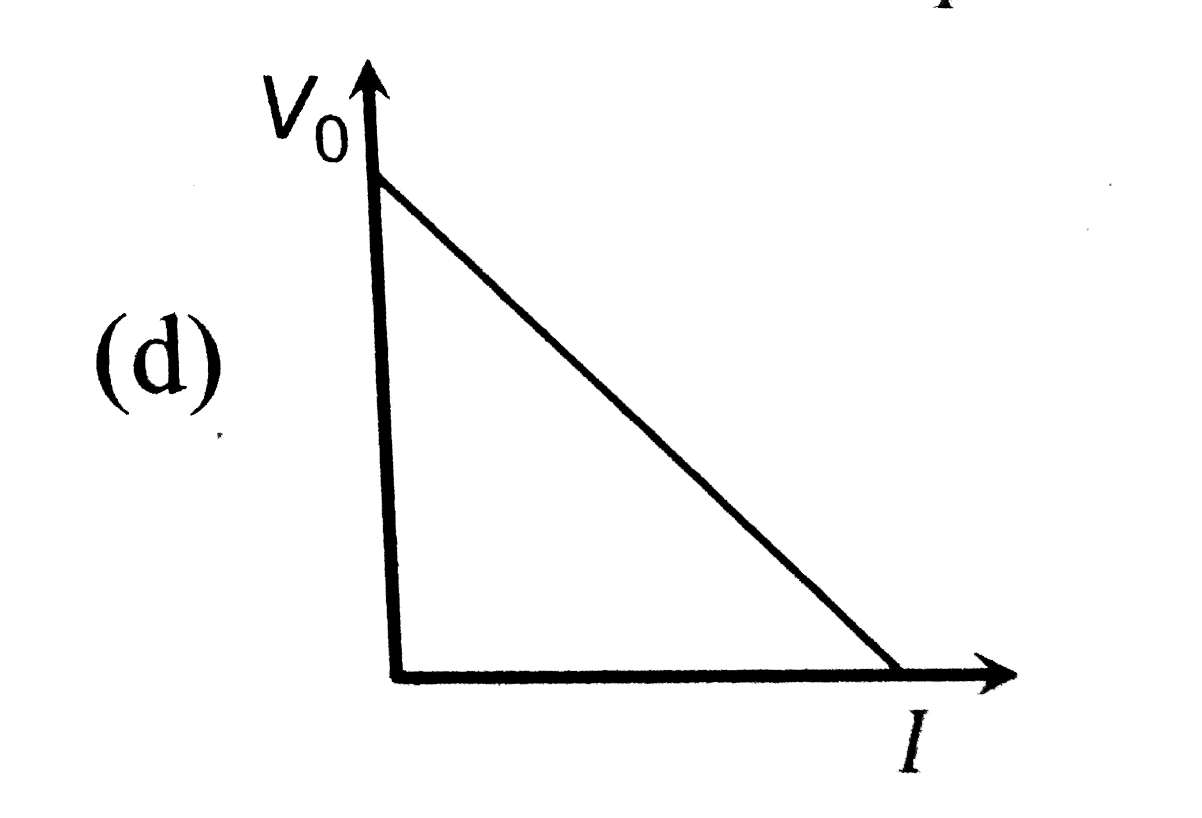
In photoelectric effect the slope of straight line graph between stopping potential (V0) and freqency of incident light (v) gives:
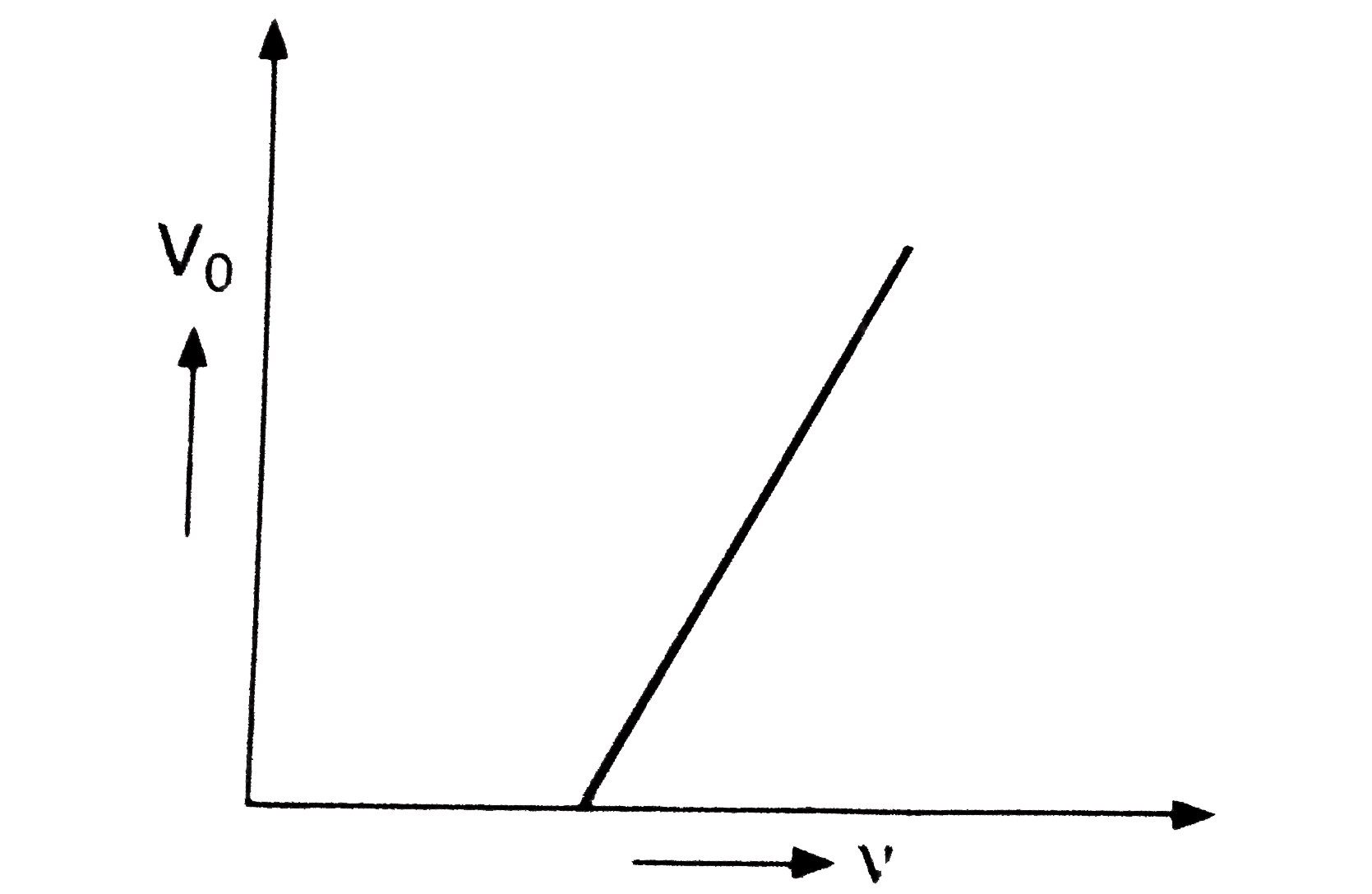 Acharge on electronBwork function of emitterCPlanck's constantDratio of Planck's constant to charge on electron
Acharge on electronBwork function of emitterCPlanck's constantDratio of Planck's constant to charge on electronThe stopping potential are V1 and V2. Calculate the (V1−V2), if the λ1 and λ2 are wavelength of incident lights, respectively.
Ahce(1λ1−1λ2)Bhce(1λ1+1λ1)Cehc(1λ1+1λ2)Dehc(1λ1−1λ2)
In photoelectric effect stopping is 3V0 for incident wavelength λ0 and stopping potential V0 for incident wavelength 2λ0. Find threshold wavelength.
View SolutionIn a photoelectric effect measurement, the stoppingg potential for a given metal is found to be V0 volt, when radiation of wavelength λ0 is used. If radiation of wavelength 2λ0 is used with the same metal, then the stopping potential (in V) will be
View SolutionIn a photoelectric effect measurement, the stoppingg potential for a given metal is found to be V0 volt, when radiation of wavelength λ0 is used. If radiation of wavelength 2λ0 is used with the same metal, then the stopping potential (in V) will be
View SolutionIn photoelectric effect experiment, the stopping potential for incident light of wavelength 4000 Å, is 3V. If the wavelength is changed to 2500 Å, the stopping potential will be
View SolutionIn an experiment of photo electric emission for incident light of 4000A0,the stopping potentail is 2V.If the wavelength of incident light is made 300A0, then the stopping potential will be
View Solution
