A ammeter of resistance 0.2Ω and range 10mA is to be used to read potential difference upto 1V. What is to be done?
96Ω in series
92Ω in parallel
99.8Ω in series
90Ω in parallel
The correct Answer is:C
To solve the problem of using an ammeter with a resistance of 0.2 Ω and a range of 10 mA to measure a potential difference of up to 1 V, we can follow these steps:
Step 1: Understand the Ammeter Specifications
The ammeter has:
- Resistance (R_a) = 0.2 Ω
- Maximum current (I_max) = 10 mA = 10 × 10^(-3) A = 0.01 A
Step 2: Calculate the Voltage Drop Across the Ammeter
The voltage drop (V_a) across the ammeter when it is at its maximum current can be calculated using Ohm's law:
Va=I×Ra
Substituting the values:
Va=0.01A×0.2Ω=0.002V
This means the ammeter can only measure a voltage drop of 2 mV at its maximum current.
Step 3: Determine the Required Voltage Measurement
We need to measure a potential difference of up to 1 V. To achieve this, we can add an additional resistance (R_g) in series with the ammeter.
Step 4: Set Up the Equation for Total Voltage
The total voltage (V_total) across the series combination of the ammeter and the additional resistance can be expressed as:
Vtotal=I×(Ra+Rg)
Where:
- V_total = 1 V (the maximum voltage we want to measure)
- I = 10 mA = 0.01 A
Step 5: Rearrange the Equation to Find R_g
Substituting the known values into the equation:
1=0.01×(0.2+Rg)
Now, solve for R_g:
1=0.002+0.01Rg
1−0.002=0.01Rg
0.998=0.01Rg
Rg=0.9980.01=99.8Ω
Step 6: Conclusion
To enable the ammeter to measure a potential difference of up to 1 V, an additional resistance of approximately 99.8 Ω must be connected in series with the ammeter.
The ammeter has:
- Resistance (R_a) = 0.2 Ω
- Maximum current (I_max) = 10 mA = 10 × 10^(-3) A = 0.01 A
The voltage drop (V_a) across the ammeter when it is at its maximum current can be calculated using Ohm's law:
Va=I×Ra
Substituting the values:
Va=0.01A×0.2Ω=0.002V
This means the ammeter can only measure a voltage drop of 2 mV at its maximum current.
We need to measure a potential difference of up to 1 V. To achieve this, we can add an additional resistance (R_g) in series with the ammeter.
The total voltage (V_total) across the series combination of the ammeter and the additional resistance can be expressed as:
Vtotal=I×(Ra+Rg)
Where:
- V_total = 1 V (the maximum voltage we want to measure)
- I = 10 mA = 0.01 A
Substituting the known values into the equation:
1=0.01×(0.2+Rg)
Now, solve for R_g:
1=0.002+0.01Rg
1−0.002=0.01Rg
0.998=0.01Rg
Rg=0.9980.01=99.8Ω
To enable the ammeter to measure a potential difference of up to 1 V, an additional resistance of approximately 99.8 Ω must be connected in series with the ammeter.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level-2
30 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - NEET Past 5 Years Questions
23 Videos
- ALTERNATING CURRENT BOOK - PHYSICS WALLAHCHAPTER - ALTERNATING CURRENT EXERCISE - NEET PAST 5 YEARS QUESTIONS
8 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
Similar Questions
A volmeter coil has resistance 50.0Ω and a resistor of 1.15kΩ is connected in series. It can read potential differences upto 12 V. If this same coil is used to construct an ammeter which can measure currents up to 2.0 A, what should be the resistance of the shunt used?
View SolutionIn the figure ammeter (i) reads a current of 10mA, while the voltmeter reads a potential difference of 3V. What does ammeter (ii) (in mA) read? The ammeters are identical, the internal resistance of the battery is negligible. (Consider all ammeters and voltmeters as non ideal)
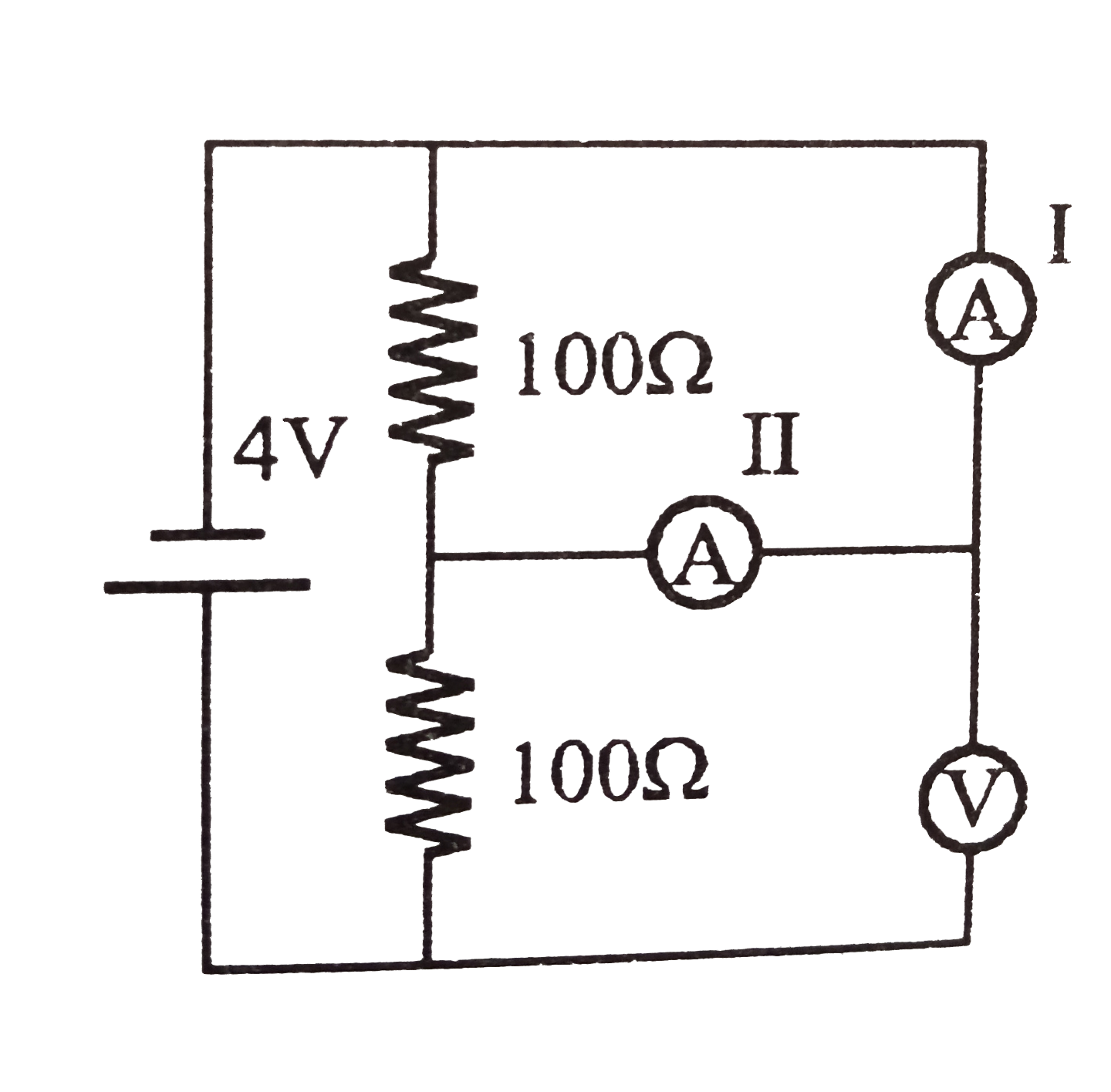
View Solution
Knowledge Check
The maximum current that can be measured by a galvanometer of resistance 40Ω is 10 mA . It is converted into a voltmeter that can read upto 50 V . The resistance to be connected in series with the galvanometer is ... (in ohm )
A2010B4050C5040D4960The maximum current that can be measured by a galvanometer of resistance 40Ω is 10 mA . It is converted into a voltmeter that can read upto 50 V . The resistance to be connected in series with the galvanometer is ... (in ohm )
A5040B4960C2010D4050An ammeter of 5Ω resistance can read 5 mA. If it is required to be used to read 100 V, the resistance needed to be connected in series will be
A19.995ΩB19995ΩC1999.5ΩD199.95Ω
A voltmeter coil has resistance 50.0(Ω)and a resistor of 1.15k(Ω)is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter which can measure currents up to 2.0A ,What should be the resistance of the shunt used ?
View SolutionA galvanometer has a resistance of 30Ω and a current of 2 mA is needed to give full scale deflection. What is the resistance needed and how is it to be connected to convert the galvanometer (i) into an ammeter of 0.3 A range and (ii) into a voltmeter of 0.2 V range?
View SolutionIn Fig. 6.76, the ammeter (I) reads a current of 10mA, while the voltmeter reads a potential difference of 3V. The ammeters are identical, and the internal resistance of the battery is negligible (consider all ammeters and voltmers as nonideal).
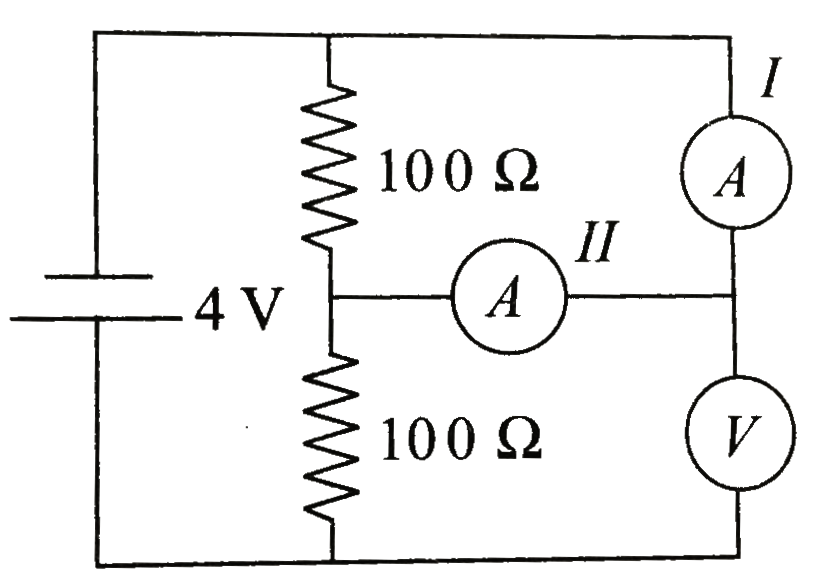
The resistance of ammeter is m×102Ω. What is the value of m ?
View SolutionA micrometer has a resistance of 10Ω and a full scale range of 50μA. It can be used as a voltmeter or a higher range ammeter provided a resistance combination (s).
View SolutionA voltmeter has resistance 2000Ω and range 0.5 V. For increasing its range upto 20V, a resistance of
View Solution
