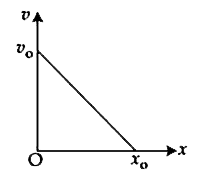
The velocity of the CM of the sytem of particle can be represented as :
vCM=∑m1v1m1
vCM=m1v1M
vCM=∑m1v1M
None of the above
To find the velocity of the center of mass (CM) of a system of particles, we can follow these steps:
1. Understanding the Center of Mass (CM):
The center of mass of a system of particles is defined as a point that represents the average position of the mass distribution in the system. The position vector Rcm of the center of mass can be expressed as:
Rcm=∑miriM
where mi is the mass of the ith particle, ri is its position vector, and M is the total mass of the system given by M=∑mi.
2. Differentiating the Position Vector:
To find the velocity of the center of mass, we need to differentiate the position vector Rcm with respect to time t:
Vcm=dRcmdt=ddt(∑miriM)
3. Applying the Derivative:
Since the total mass M is constant (assuming no mass is added or removed), we can take it out of the derivative:
Vcm=1M∑midridt
Here, dridt is the velocity vi of the ith particle.
4. Substituting Velocities:
Thus, we can rewrite the equation:
Vcm=1M∑mivi
5. Final Expression:
The final expression for the velocity of the center of mass is:
Vcm=∑miviM
where M=∑mi is the total mass of the system.
Conclusion:
The velocity of the center of mass of a system of particles can be represented as:
Vcm=∑miviM
The center of mass of a system of particles is defined as a point that represents the average position of the mass distribution in the system. The position vector Rcm of the center of mass can be expressed as:
Rcm=∑miriM
where mi is the mass of the ith particle, ri is its position vector, and M is the total mass of the system given by M=∑mi.
To find the velocity of the center of mass, we need to differentiate the position vector Rcm with respect to time t:
Vcm=dRcmdt=ddt(∑miriM)
Since the total mass M is constant (assuming no mass is added or removed), we can take it out of the derivative:
Vcm=1M∑midridt
Here, dridt is the velocity vi of the ith particle.
Thus, we can rewrite the equation:
Vcm=1M∑mivi
The final expression for the velocity of the center of mass is:
Vcm=∑miviM
where M=∑mi is the total mass of the system.
The velocity of the center of mass of a system of particles can be represented as:
Vcm=∑miviM
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
- THERMAL PROPERTIES OF MATTER BOOK - PHYSICS WALLAHCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - NEET Past 5 Years Questions
12 Videos
Similar Questions
Knowledge Check
The velocity of the CM of the system of particles can be represented as :
AvCM=∑m1v1m1BvCM=m1v1MCvCM=∑m1v1MDNone of the aboveA particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2
Mirror is moving towards the particle with speed 2 cm/sec. Speed of A ad B are 10√2 and 5 cm/sec respectively in the direction shown in figure. Magnitude of velocity of image of the particle B with respect to image of A.A√325cm/secB15cm/secC13cm/secD√269cm/sec
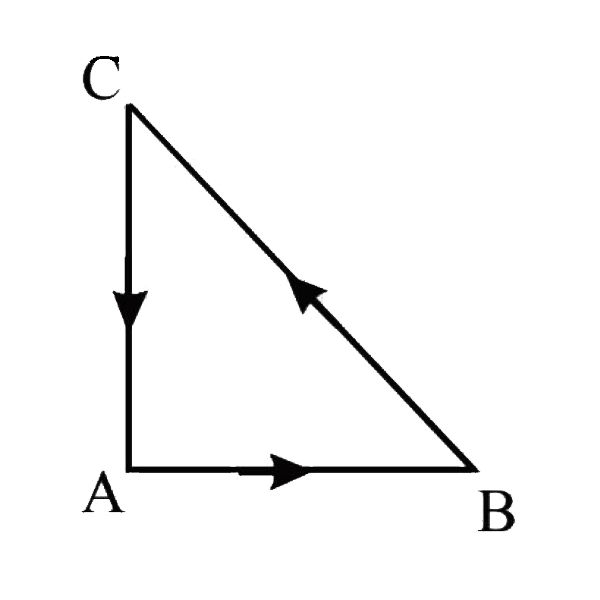
Three forcesstart acting simultaneously on a particle moving with a velocity →v . These forces are represented in magnitude and direction by three sides of a triangle taken in the same order. What now will be the velocity of the particle ?
View SolutionThree forces start acting simultaneously on a particle moving with velocity, ¯v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
View SolutionFigure below shows the velocity-time graph of a one dimensional motion. Which of the following characteristic of the particle is represented by the shaded area?

View SolutionA particle is executing simple harmonic motion with an angular at a 4cm. At the mean position the velocity of the particle is 10cm/sec .The particle from the mean position when its speed becomes 2cm/s is
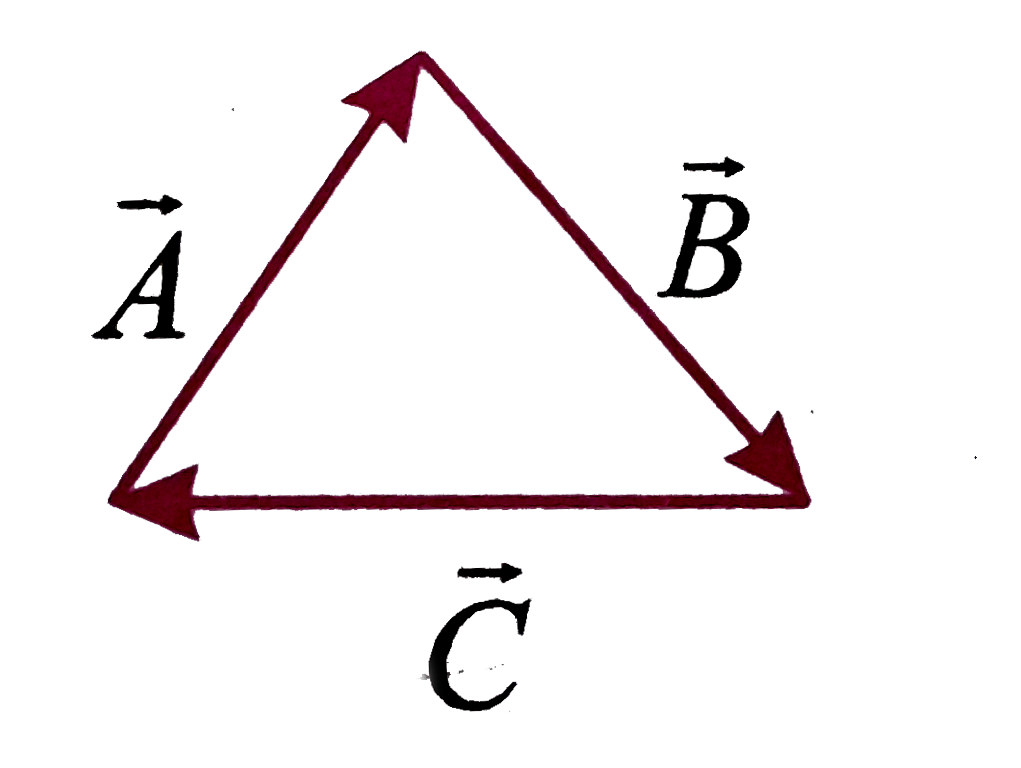
View SolutionThree forces start acting simultaneously on a particle moving the velocity →V. The forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity
View Solution