A disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
I1ω1I2
I2ω1I2+I2
I1ω2I1+I2
(I1+I2)I2ω1
According toe the consevation of angular momentum Iω= constant
When second disc is dropped on it and forms a unit.
I1ω1=(I1+I2)ω2
(angular momentum always constant )
I1ω1I1+I2=ω2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - LEVEL-2
30 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
- THERMAL PROPERTIES OF MATTER BOOK - PHYSICS WALLAHCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - NEET Past 5 Years Questions
12 Videos
Similar Questions
A disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View Solution
Knowledge Check
A disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
AI1ω1I2BI2ω1I2+I2CI1ω2I1+I2D(I1+I2)I2ω1A circular disk of moment of inertia It is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disc to friction is
A12I2b(It+Ib)ω2iB12I2t(Ii+Ib)ω2iCIb−It(It+Ib)ω2iD12IbIt(It+Ib)ω2iThe two uniform discs rotate separately on parallel axles. The upper disc (radius a and momentum of inertia I1) is given an angular velocity ω0 and the lower disc of (radius b and momentum of inertia I2) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
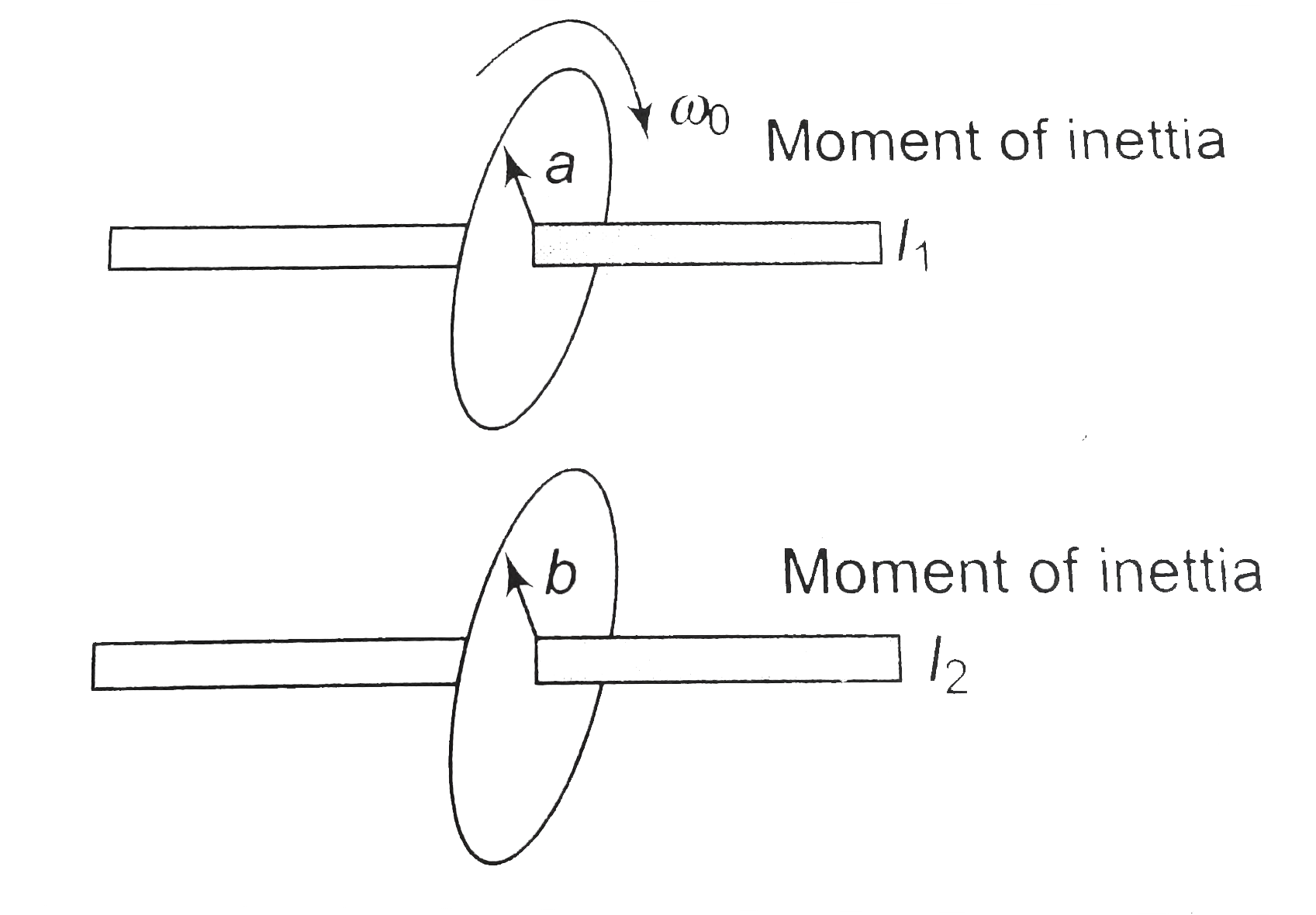 .A(I1ω0)[I1+(a2I2/b2)]B(I2ω0)[I2+(a2I1/b2)]C(I1ω0)[I1+(b2I2/a2)]D(I2ω0)[I2+(b2I2/a2)]
.A(I1ω0)[I1+(a2I2/b2)]B(I2ω0)[I2+(a2I1/b2)]C(I1ω0)[I1+(b2I2/a2)]D(I2ω0)[I2+(b2I2/a2)]
A disc with moment of inertiaI1, is rotating with an angular velocity ω1 about a fixed axis. Another coaxial disc with moment of inertia I2, which is at rest is gently placed on the first disc along the axis. Due to friction discs slips against each other and after some time both disc start rotating with a common angular velocity. Find this common angular velocity.
View SolutionA disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionA disc of the moment of inertia 'l1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1' . Another disc of moment of inertia 'I2'. having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is
View SolutionA torque T acts on a body of moment of inertia l rotating with angular speed ω. It will be stopped just after time
View SolutionA disk with moment of inertia I1 rotates about frictionless, vertical axle with angular speed ωi A second disk, this one having moment of inertia I2 and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed ωf. The value of ωf is.
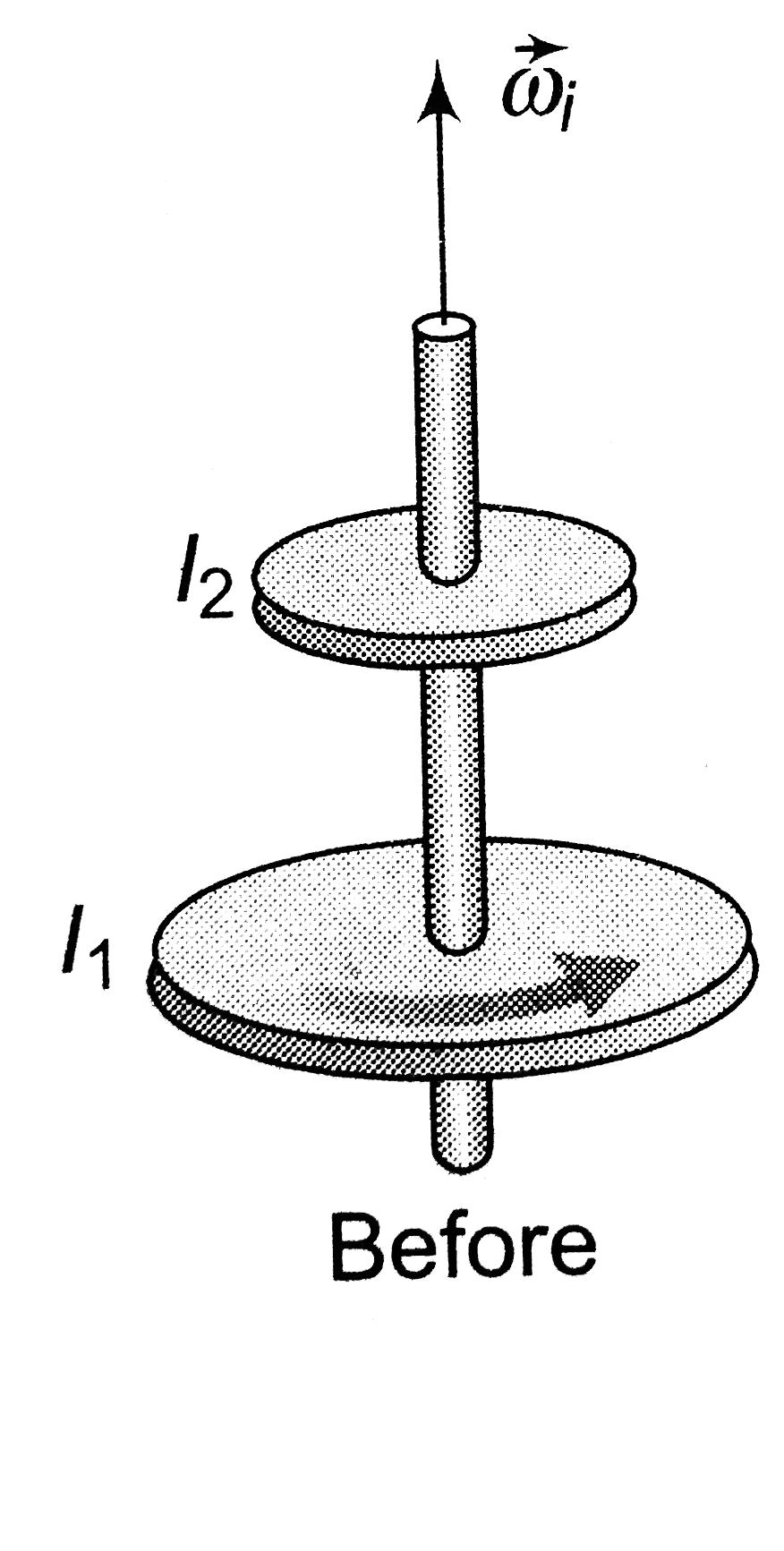 .
.
View Solution
