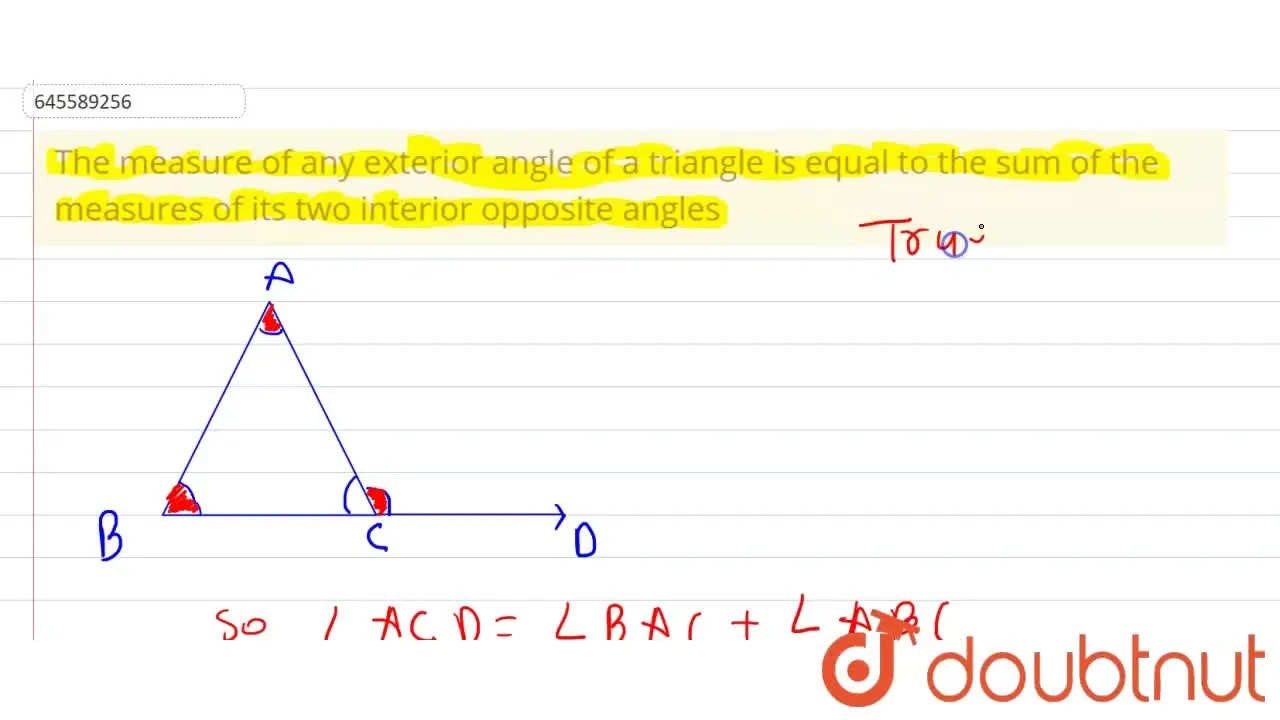
The measure of any exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles
The correct Answer is:1
Step by step video, text & image solution for The measure of any exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Related Playlists
Similar Questions
find the sum of all exterior angles of a triangle.
View Solution27.Prove that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
View SolutionFill in the blanks to make the following statements true: Sum of the angles of a triangle is ............ An exterior angle of a triangle is equal to the two ............ opposite angles. An exterior angle of a triangle is always ............ than either of the interior opposite angles. A triangle cannot have more than ............ right angles. A triangles cannot have more than ............ obtuse angles.
View SolutionExterior angle of a triangle is always ____ then either of its interior opposite angles .
View SolutionExterior angle theorem : If a side of a triangle is produced; the exterior angle so formed is equal to the sum of the two interior opposite angles.
View SolutionTheorem 6.8 : If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
View SolutionHow many sides does a polygon have if the sum of the measures of its internal angles is five times as large as the sum of the measures of its exterior angles ?
View SolutionTHEOREM (Exterior Angle Property of a Triangle) : If a side of a triangle is produced the exterior angle so formed is equal to the sum of two interior opposite angles.
View SolutionThe ratio of the measure of an exterior angle of a regular nonagon to the measure of one of its interior angles is:
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View Solution