In a certain region of space, the potential field depends on x and y-coordinates as $V = (- x^{2} + y^{2})$ . The corresponding electric field lines in xy-plane are correctly represented by

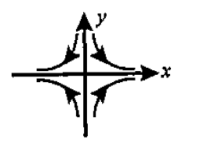
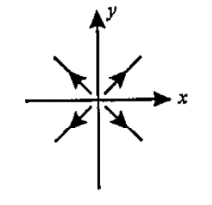
ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the electric field corresponding to the given potential field $V = - x^{2} + y^{2}$ . The electric field $E$ is related to the electric potential $V$ by the equation:
$E = - \nabla V$
where $\nabla V$ is the gradient of the potential $V$ . In two dimensions, the gradient can be expressed as:
$\nabla V = (\frac{\partial V}{\partial x}, \frac{\partial V}{\partial y})$
Step 1: Calculate the partial derivative of $V$ with respect to $x$
The potential function is given by:
$V = - x^{2} + y^{2}$
Now, we differentiate $V$ with respect to $x$ :
$\frac{\partial V}{\partial x} = \frac{\partial}{\partial x} (- x^{2} + y^{2}) = - 2 x$
Step 2: Calculate the partial derivative of $V$ with respect to $y$
Next, we differentiate $V$ with respect to $y$ :
$\frac{\partial V}{\partial y} = \frac{\partial}{\partial y} (- x^{2} + y^{2}) = 2 y$
Step 3: Write the components of the electric field
Using the relation $E = - \nabla V$ , we can find the components of the electric field:
$E_{x} = - \frac{\partial V}{\partial x} = - (- 2 x) = 2 x$
$E_{y} = - \frac{\partial V}{\partial y} = - 2 y$
Thus, the electric field vector can be expressed as:
$E = (2 x, - 2 y)$
Step 4: Analyze the electric field lines
To analyze the electric field lines, we can express the relationship between $E_{x}$ and $E_{y}$ :
$\frac{E_{y}}{E_{x}} = \frac{- 2 y}{2 x} = - \frac{y}{x}$
This implies that the electric field lines can be represented by the equation:

y = -kx \quad \text{(where k is a constant)}
This indicates that the electric field lines are straight lines passing through the origin with a negative slope.
Step 5: Identify the correct representation among the options
From the options provided, we need to identify which graph represents straight lines with a negative slope. The correct representation will be the one that shows straight lines in the xy-plane.
Final Answer
The correct representation of the electric field lines in the xy-plane is option B.
---

Updated on:18/9/2024

In a certain region of space, the potential is given by $V = k (2 x^{2} - y^{2} + z^{2})$ . The electric field at the point (1, 1, 1) has magnitude:
A $k \sqrt{6}$
B $2 k \sqrt{6}$
C $2 k \sqrt{3}$
D $4 k \sqrt{3}$
In a certain region of space , the potential is given by : $V = K [2 x^{2} - y^{2} - y^{2} z^{2}]$ . The electric field at the point (1.1.1) has magnitude =.
A $k \sqrt{6}$
B $2 k \sqrt{6}$
C $2 k \sqrt{3}$
D $4 k \sqrt{3}$
In a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constant
BPositive
CNegative
DZero