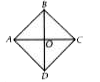
If ABCD is rhombus, then find the correct statement:

$A C^{2} + B D^{2} = 6 A B^{2}$

$A C^{2} + B D^{2} = 4 A B^{2}$

$A C^{2} + B D^{2} = 3 A B^{2}$

$A C^{2} + B D^{2} = 2 A B^{2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem step by step, we will analyze the properties of a rhombus and apply the Pythagorean theorem to find the correct statement.
1. Understand the Properties of a Rhombus:
- A rhombus is a quadrilateral with all sides equal. Therefore, we have:
$A B = B C = C D = D A$
2. Diagonals of a Rhombus:
- The diagonals of a rhombus bisect each other at right angles (90 degrees). Let the diagonals be $A C$ and $B D$ . The intersection point of the diagonals is $O$ .
- Thus, we can express:
$O A = O C = \frac{A C}{2} and O B = O D = \frac{B D}{2}$
3. Consider Triangle AOB:
- Since $∠ A O B = 90^{\circ}$ , we can apply the Pythagorean theorem:
$A B^{2} = O A^{2} + O B^{2}$
4. Substituting the Values:
- Substitute $O A$ and $O B$ with their respective expressions:
$A B^{2} = {(\frac{A C}{2})}^{2} + {(\frac{B D}{2})}^{2}$
- This simplifies to:
$A B^{2} = \frac{A C^{2}}{4} + \frac{B D^{2}}{4}$
5. Combine the Terms:
- Multiply the entire equation by 4 to eliminate the fractions:
$4 A B^{2} = A C^{2} + B D^{2}$
6. Identify the Correct Statement:
- From the derived equation, we can see that:
$A C^{2} + B D^{2} = 4 A B^{2}$
- Therefore, the correct statement is:
$A C^{2} + B D^{2} = 4 A B^{2}$
Conclusion:
The correct statement regarding the rhombus is:
$A C^{2} + B D^{2} = 4 A B^{2}$

Updated on:18/9/2024