A piece of paper is in the form of a sector, making an angle a. The paper is rolled to form a right circular cone of radius 5 cm and height 12 cm. Then the value of angle a is
10π13
9π13
5π13
6π13
To find the value of angle a when a piece of paper in the form of a sector is rolled to form a right circular cone, we can follow these steps:
Step 1: Identify the dimensions of the cone
We are given:
- Radius of the cone r=5 cm
- Height of the cone h=12 cm
Step 2: Calculate the slant height of the cone
The slant height l can be calculated using the Pythagorean theorem:
l=√h2+r2
Substituting the values:
l=√122+52=√144+25=√169=13 cm
Step 3: Relate the slant height to the angle of the sector
When the sector is rolled into a cone, the slant height of the cone corresponds to the radius of the sector. Therefore, the radius of the sector is equal to the slant height l.
Step 4: Calculate the circumference of the base of the cone
The circumference C of the base of the cone can be calculated as:
C=2πr=2π×5=10π cm
Step 5: Relate the circumference to the angle of the sector
The angle a in radians can be found using the formula:
Arc length=r⋅a
Where the arc length is equal to the circumference of the base of the cone. Thus, we have:
10π=13⋅a
Step 6: Solve for angle a
Now, we can solve for a:
a=10π13
Conclusion
The value of angle a is:
a=10π13 radians
---
We are given:
- Radius of the cone r=5 cm
- Height of the cone h=12 cm
The slant height l can be calculated using the Pythagorean theorem:
l=√h2+r2
Substituting the values:
l=√122+52=√144+25=√169=13 cm
When the sector is rolled into a cone, the slant height of the cone corresponds to the radius of the sector. Therefore, the radius of the sector is equal to the slant height l.
The circumference C of the base of the cone can be calculated as:
C=2πr=2π×5=10π cm
The angle a in radians can be found using the formula:
Arc length=r⋅a
Where the arc length is equal to the circumference of the base of the cone. Thus, we have:
10π=13⋅a
Now, we can solve for a:
a=10π13
The value of angle a is:
a=10π13 radians
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of a right circular cone is 3 cm and its height is 4 cm. The total surface area of the cone is
A48.4 sq. cmB64.4 sq. cmC96.4 sq. cmD75.4 sq. cm - Question 2 - Select One
A piece of paper in the shape of a sector of a circle (see Fig. 1) is rolled up to form a right- circular cone (see Fig. 2). The value of the angle θ is.
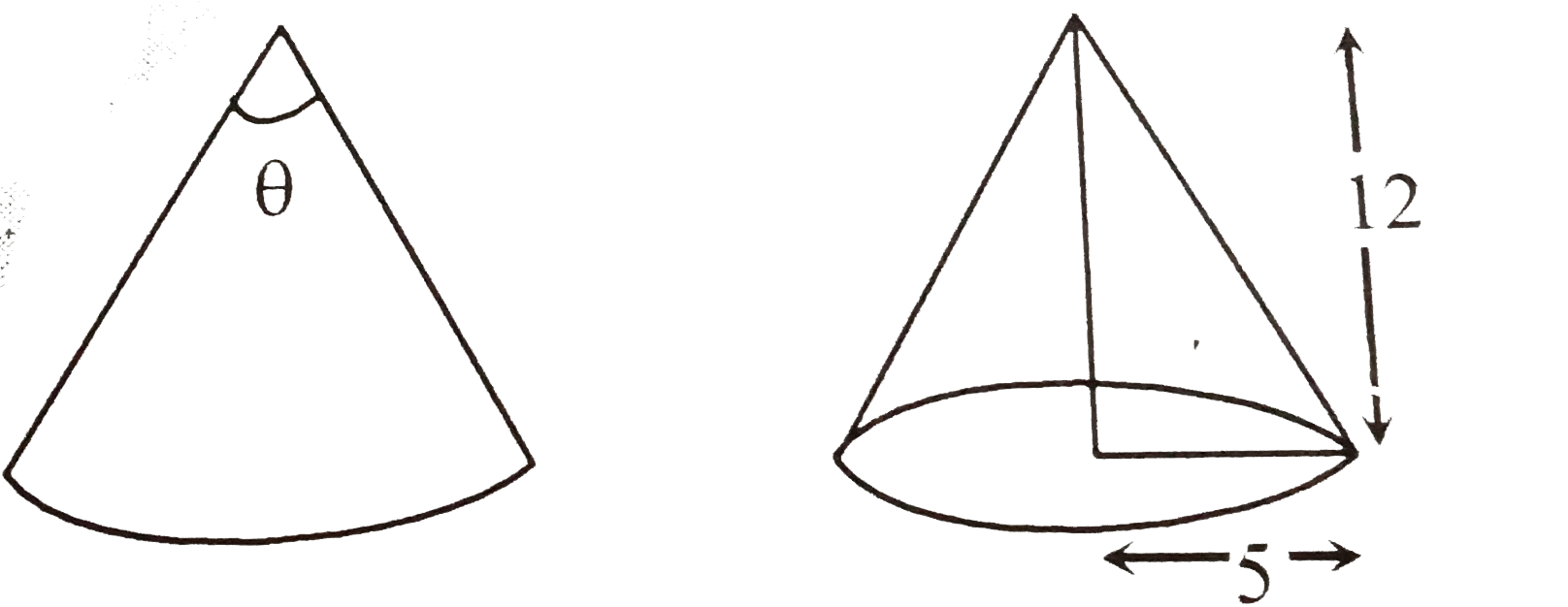 A10π13B9π13C5π13D6π13
A10π13B9π13C5π13D6π13 - Question 3 - Select One
The volume of a right circular cone of height 12cm and base radius 6cm, is
A(12π)cm3B(36π)cm3C(72π)cm3D(144π)cm3
The radius of the base of a solid right circular cone is 8 cm and its height is 15 cm. The total surface area of the cone is:
View SolutionThe curved surface area of the cone of radius 5 cm and height 12 cm is
View SolutionA sector is formed by opening out a cone of base radius 8 cm and height 6 cm. Then the radius of the sector is (in cm)
View SolutionThe volume of a right circular cone is 100 π cm3 and its height is 12 cm. Find its slant height.
View SolutionFind the total surface area (in cm2) of a right circular cone of diameter 28 cm and slant height 12 cm.
View Solution

