Let PQ be a focal chord of the parabola y2=4ax. The tangents to the parabola at P and Q meet at point lying on the line
y=2x+a,a<0.
The length of chord PQ is Solution in Tamil
7a
5a
2a
3a
The correct Answer is:B
Since, R[−a,a(r−1t)] lies on y=2x+a.
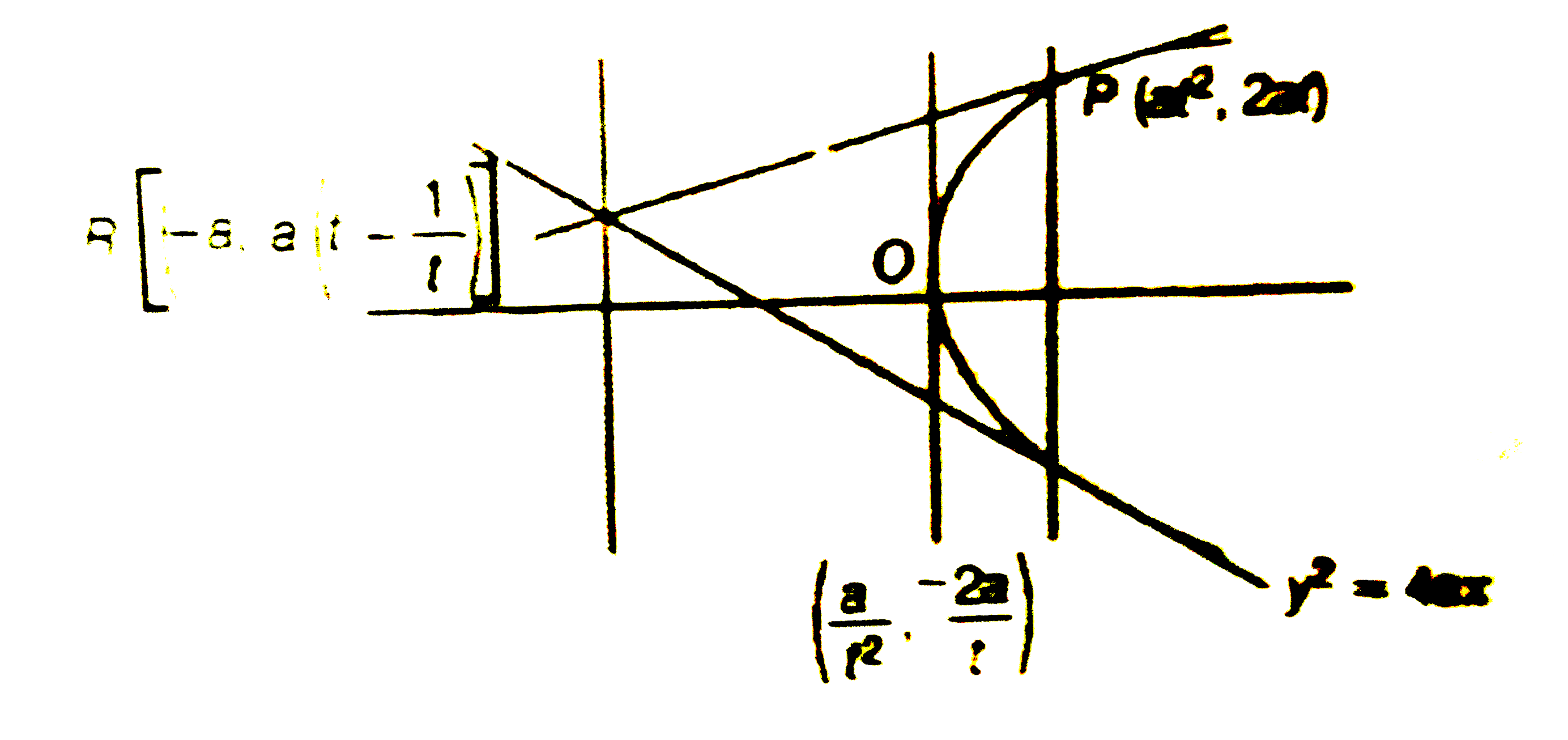
⇒a(t−1t)=−2a+a⇒t−1t=−1
Thus, length of focal chord
=a(t+1t)2=a{(t−1t)2+}=5a
Similar Questions
Let PQ be a focal chord of the parabola y^2 = 4ax The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0 . Length of chord PQ is
View SolutionLet PQ be a focal chord of the parabola y^(2)=4ax . The tangents to the parabola at P and Q meet at point lying on the line y=2x+a,alt0 . If chord PQ subtends an angle theta at the vertex of y^(2)=4ax , then tantheta=
View Solutionमाना कि PQ परवलय y2=4ax की एक नाभिय जीवा है। बिन्दुओं P तथा Q पर परवलय की स्पर्श रेखाएँ एक बिन्दु पर मिलती है जो कि रेखा y=2x+a,a>0 पर स्थित है।
जीवा PQ की लम्बाई है :
View SolutionLet PQ be the parabola y^2=4ax Is a focal chord. The tangent lines of the parabola on the points P and Q meet at a point which is the line y=2x + a, a gt0 Is located at. The length of chord PQ is
View SolutionLet PQ be a focal chord of the parabola y^2 = 4ax The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0 . Length of chord PQ is
View SolutionLet PQ be a focal chord of the parabola y^(2)=4ax . The tangents to the parabola at P and Q meet at point lying on the line y=2x+a,alt0 . If chord PQ subtends an angle theta at the vertex of y^(2)=4ax , then tantheta=
View SolutionLet PQ be a focal chord of the parabola y^2 = 4ax The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0 . Length of chord PQ is
View SolutionLet PQ be a focal chord of the parabola y^2 = 4ax The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0 . Length of chord PQ is
View Solution
