If the normals of the paralbola y^2=4x drawn at the end points of its latus rectum are tangents to the circle (x-3)^(2) + (y+2)^(2) = r^(2) then the value of r^(2) is Solution in Tamil
The correct Answer is:2
End points of latusrectum are (a±2a) i.e. (1±2)
Equation of normal at (x1,y1) is
y−y1x−x1=y12a
i.e., y−2x−1=−22 and y+2x−1=23
⇒x+y+3
and x−y=3
Which is tangent to (X−3)2+(y+2)2=r2
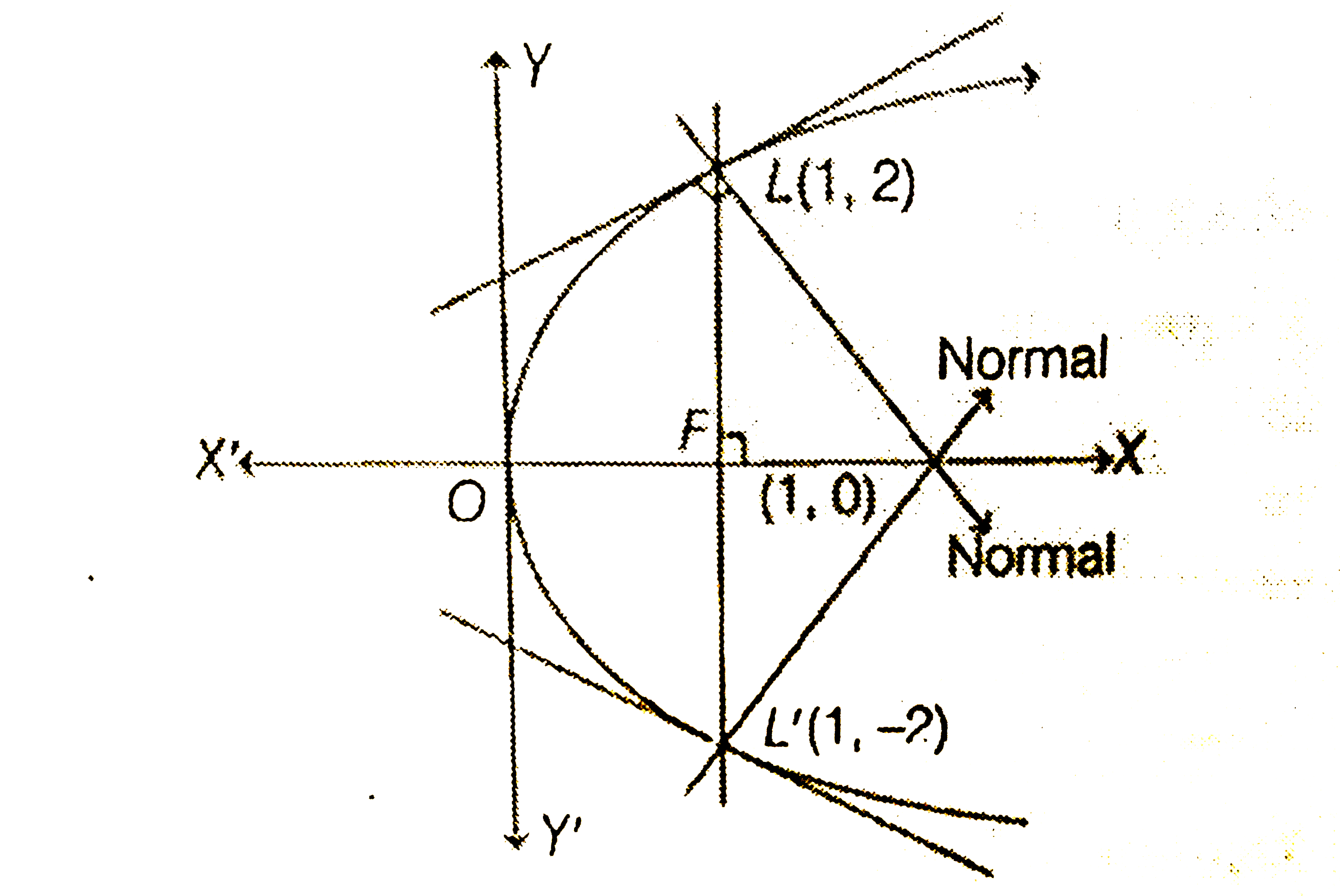
∴ Length of perpendicular from centre = Radius
⇒|3−2−3|√12+12=r
∴r2=2
Similar Questions
·If the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2(y+2)2=r2 , then the value of r2 is
View Solution·If the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2(y+2)2=r2 , then the value of r2 is
View SolutionIf parabola y^2 = 4x The nomals circle drawn at the vertex of the latus rectum (x-3)^2+(y+2)^2=r^2 Are the tangent lines of r^2 The value of
View Solutionयदि परवलय (parabola) y2=4x के नाभिलम्ब जीवा (latus rectum) के शिखर बिन्दुओं पर खीचें गए अभिलम्ब (normals) वृत्त (x−3)2+(y+2)2=r2, की स्पर्श रेखाऐं हैं तब r2 का मान है
View SolutionIf the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2+(y+2)2=r2 is
View SolutionCircle is drawn with end points of latus rectum of the parabola y2=4ax as diameter, then equation of the common tangent to this circle & the parabola y2=4ax is :
View SolutionIf the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2+(y+2)2=r2, then the value of r4 is equal to
View SolutionIf the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2+(y+2)2=r2 , then the value of r2 is
View Solution
