The solution of the differential equation dydx=2xy isSolution in Tamil
A
intersects y = x + 2 exactly at one point
B
intersects y = x + 2 exactly at the two points
C
intersects y = (x+2)2
D
does not intersect y=(x+3)2
Video Solution
Text Solution
The correct Answer is:A, D
Given, (x2+xy+4x+2y+4)dydx−y2=0
⇒[(x2+4x+4)+y(x+2)]dydx−y2=0
⇒[(x+2)2+y(x+2)]dydx−y2=0
Put x + 2 = X and y = Y, then
(X2+XY)dYdX−Y2=0
⇒X(2) dY + XYdY - Y^(2) dX = 0<br>implies X2dY+Y(XdY−YdX)=0
⇒−dYY=XdY−YdXX2
⇒−d(log|Y|)=d(YX)
On integrating both sides, we get
−log|Y|=YX+C, where x+2=X
and y=Y
⇒−log|y|=(y)=yx+2+C
Since, it passes through the point (1,3)
∴−log3=1+C
⇒C=−1−log3=−(loge+log3)=−log3e
∴ Eq (i) becomes
log|y|+yx+2−log(3e)=0
⇒log(|y|3e)+Yx+2=0
Now, to check option (a), y = x + 2 intersects the curve.
⇒log(|x+2|3e)+x+2x+2=0
⇒log(|x+2|3e)=−1
⇒|x+2|3e=e−1=1e
⇒|x+2|=3 or x+2=±3
∴x=1, -5 (rejected) =, as x>0
∴x=1 only one solution.
Thus, (a) is the correct answer.
To check option (c ), we have
y=(x+2)2 and log.(|y|3e)+yx+2=0
⇒log[|x+2|23e]+(x+2)2x+2=0
⇒log[|x2|23e]=−(x+2)
⇒(x+22)3e=e−(x+2) or (x+2)2ex+2=3e
⇒ex+2=3e(x+2)3
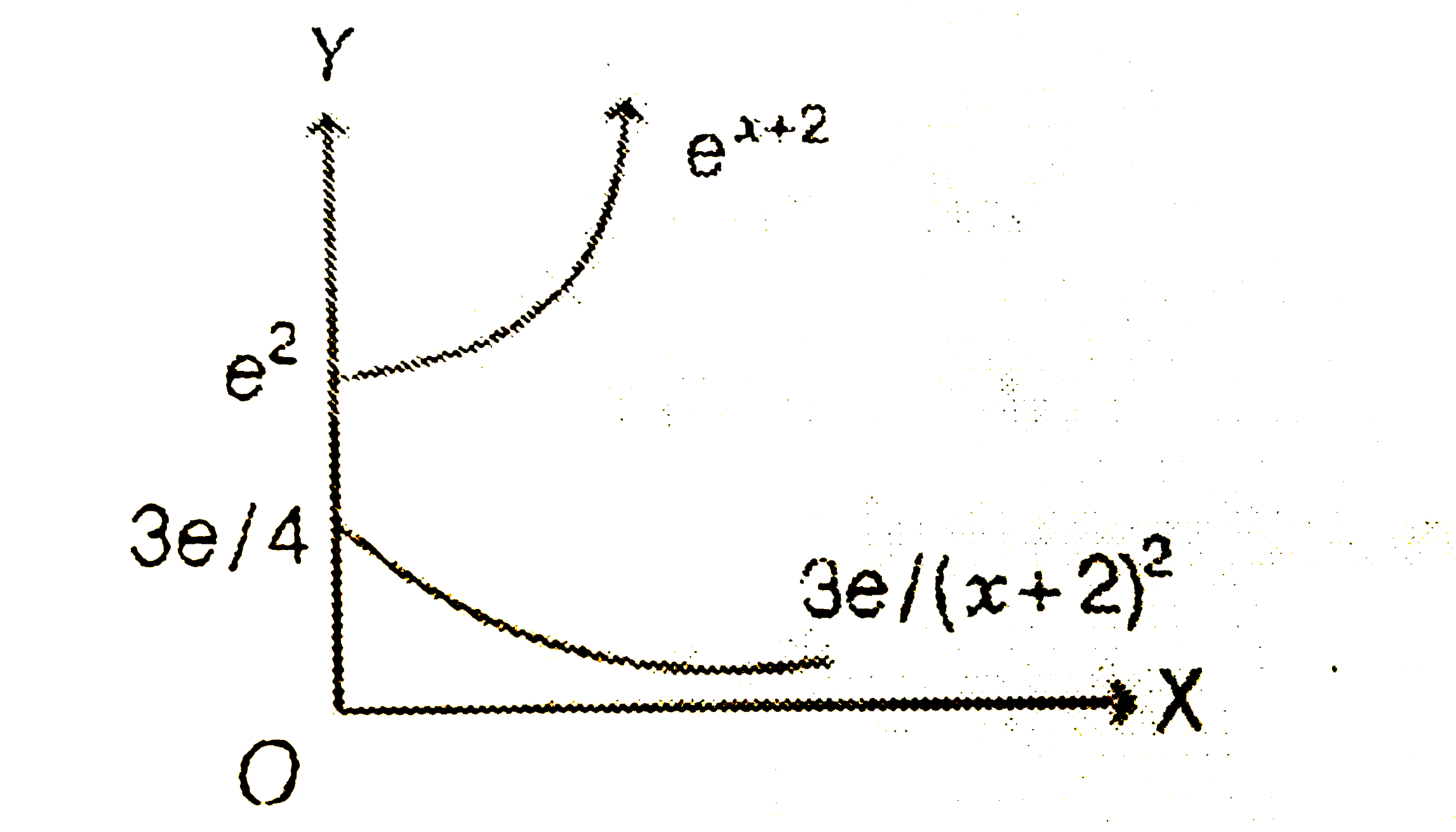
Clearly, they have no solution.
To check option (d), y=(x+3)2
i.e., log[|x+3|23e]+(x+3)2(x+2)=0
To check the number of solutions.
Let g(x)=2log(x+3)+(x+3)2(x+2)−log(3e) ltbr ∴g'(x)=2x+3+((x+2).2(x+3)−(x+3)2.1(x+2)2−0
=2x+3+(x+3)(x+1)(x+2)2
Clearly, when x>0, then g'(x)>0
∴ g (x) in increasing, when x>0
Thus, when x>0, then g (x) > g (0)
g(x)>log(3e)+94>0
Hence, there is no solution
Thus, option (d) is true.
|
Similar Questions
The solution of the differential equation dydx−2xy1+x2=0 is
View Solutionअवकल समीकरण dydx=2xy का हल है
View Solutionअवकल समीकरण dydx+2xy=e−x2 का हल ज्ञात कीजिये।
View Solutiondydx=2xy எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வு
View SolutionThe solution of the differential equation 2xydydx=x2+3y2 is
View Solutionअवकल समीकरण x2dy=−2xydx का व्यापक हल है
View Solutionअवकल समीकरण dydx+2xy=y का हल है
View SolutionThe equation of differential equation 2xydydx=y2−x2 is :
View Solution
