Find the shortest distance of the point (0,c) from the parabola y=x2,where0≤c≤5.Solution in Tamil
Video Solution
Text Solution
The correct Answer is:√c−14,12≤c≤5
Let the point Q (x,x2) on x2=y whose distance from (0,c) is minimum.
Now PQ2=x2+(x2−c)2
Let f(x)=x2+(x2−c)2
f'(x)=2x+2(x2−c)2x
=2x(1+2x2−2c)=4x(x2−c+12)
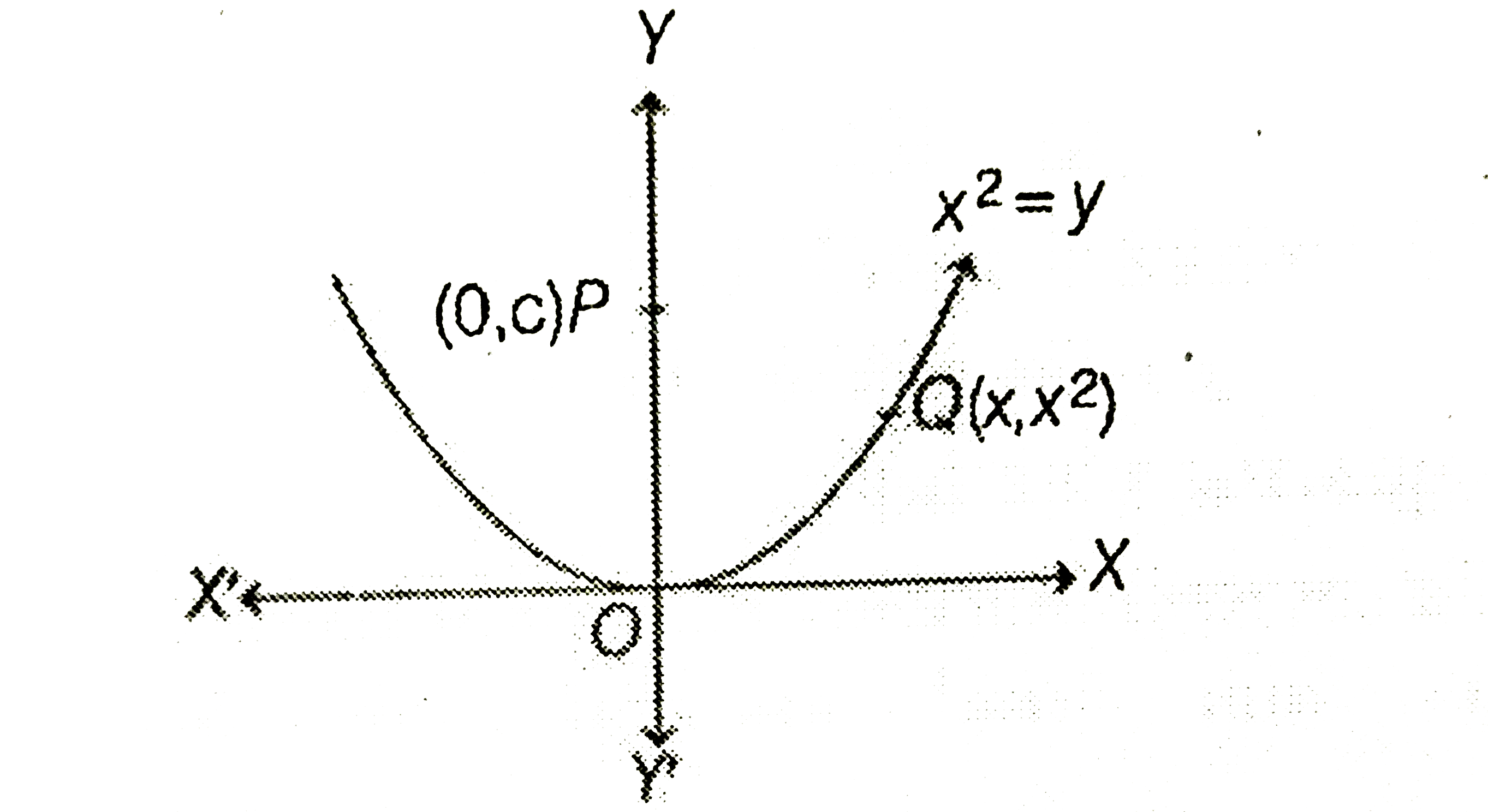
4x(x−√c−12)(x+√c−12), when c>12
For maxima put f'(x)=0
Now, f''(x)=4[x2−c+12]+4x[2x]
At x=±√c−12
f''(x)≥0
∴f(x) is minimum
Hence, minimum value of f(x)=|PQ|
⎷(√c−12)2+((srt(c−12))2−c)2
=√c−12+(c+12−c)2=√c−14,12≤c≤5
|
Similar Questions
Solve for xandy:√3sinx+cosx=8y−y2−18,where0≤x≤4π,y∈R
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2 , where 0≤c≤5 .
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2, where 0≤c≤5.
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2 , where 0≤c≤5 .
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2, where 12≤c≤5.
View SolutionFind the shortest distance of the point (0,c) from the parabola y=x2 where 0≤c≤5
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2 , where 0≤c≤5 .
View SolutionFind the shortest distance of the point (0, c) from the parabola y=x2, where 0≤c≤5.
View Solution
