Tangent and normal are drawn at P(16,16) on the parabola y2=16x, which intersect the axis of the parabola at A and B, espectively. If C is the centre of the circle through the points P,A and B and ∠CPB=θ, then a value of tanθ is Solution in Tamil
12
2
3
43
The correct Answer is:B
Equation of tangent and normal to the curve y2=16x at (16, 16) is x−2y+16=0 and 2x+y−48=0 respectively.
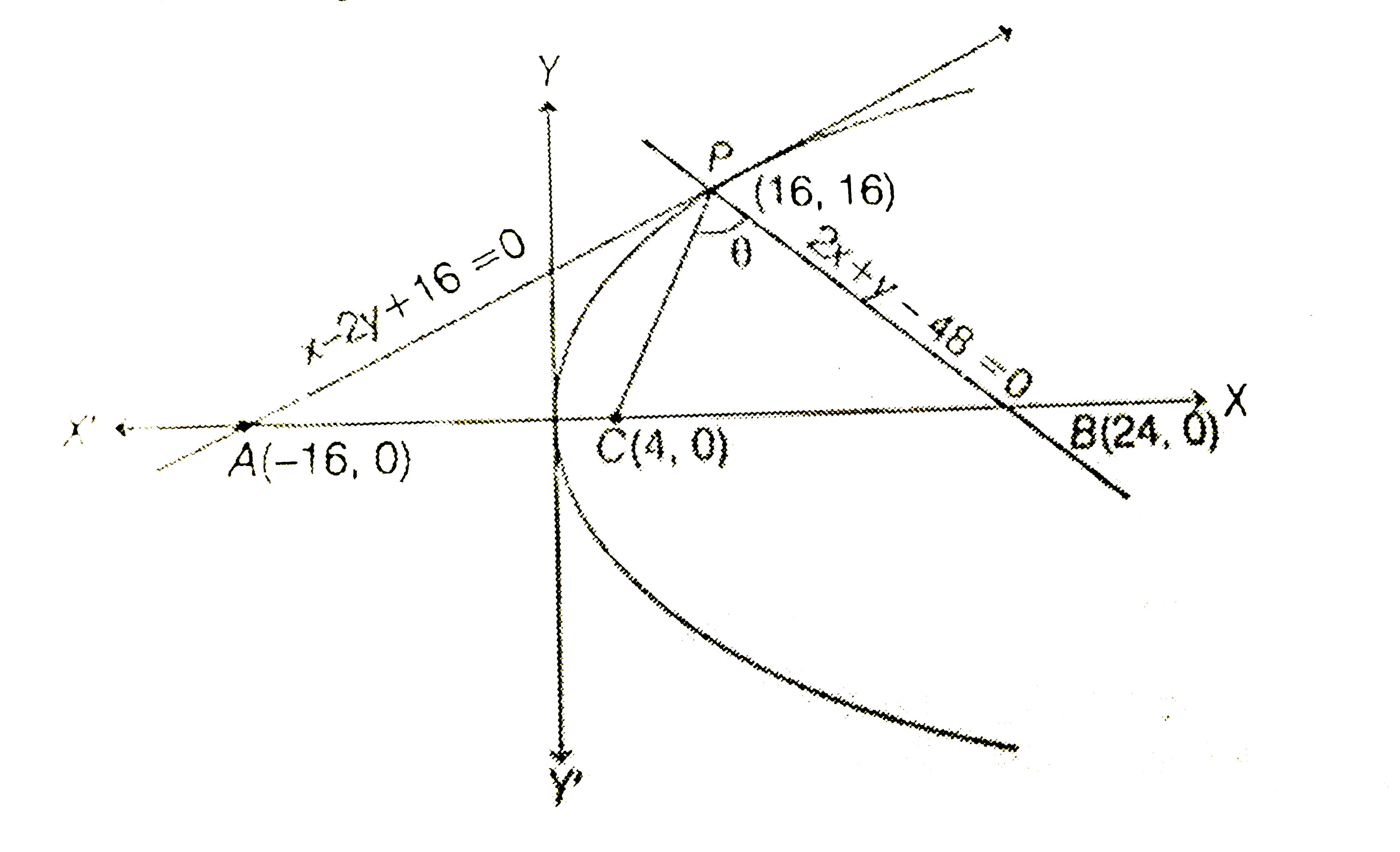
A=(−16,0)B=(24,0)
∵C is the centre of circle passing through PAB i.e.,
Slope of PC=16−016−4=1612=43=m1
Slope of PB=16−016−24=16−8=−m2
tanθ=∣∣∣m1−m21+m1m2∣∣∣
⇒tanθ=∣∣
∣
∣∣43+21−(43)(2)∣∣
∣
∣∣⇒tanθ=2
Similar Questions
Tangent and normal from point P(16, 16) to the parabola y2=16x intersects the axis of parabola of points A and B. If C is the centre of the circle from points P,A and B. Such that ∠CPB=θ then one possible value of θ is ……….
View Solutionपरवलय y2=16x के एक बिन्दु P(16, 16) पर स्पर्श रेखा तथा अभिलम्ब खींचे जाते हैं तो परवलय के अक्ष को दो बिन्दुओं क्रमशः A तथा B पर प्रतिच्छेद करते हैं। यदि बिन्दुओं P, A तथा B से होकर जाने वाले वृत्त का केन्द्र C है तथा ∠CPB=θ हो, तो tanθ का मान है:
(i) 3 (ii) 43 (iii) 12 (iv) 2
View SolutionTangent and normal are drawn at P(16,16) on the parabola y^2=16x which intersect the axis of the parabola at A and B respectively. If C is the centre of the circle through the points P,A and B and angle CPB=theta then the value of tan theta is
View Solutionपरवलय y2=16x के एक बिन्दु P(16,16) पर स्पर्शरेखा तथा अभिलम्ब खींचे जाते हैं तो परवलय के अक्ष को बिन्दुओं क्रमश: A तथा B पर प्रतिच्छेद करते हैं। यदि बिन्दुओं P, A तथा B से होकर जाने वाले वृत्त का केन्द्र C है तथा ∠CPB=θ, तो tanθ का मान है
View SolutionA circle is drawn having centre at C (0,2) and passing through focus (S) of the parabola y^2=8x , if radius (CS) intersects the parabola at point P, then
View SolutionTangent and normal are drawn at P(16,16) on the parabola y^2=16x which intersect the axis of the parabola at A and B respectively. If C is the centre of the circle through the points P,A and B and angle CPB=theta then the value of tan theta is
View SolutionTangent and normal are drawn at the point P-=(16 ,16) of the parabola y^2=16 x which cut the axis of the parabola at the points A and B , respectively. If the center of the circle through P ,A and B is C , then the angle between P C and the axis of x is
View SolutionA circle is drawn having centre at C (0,2) and passing through focus (S) of the parabola y^2=8x , if radius (CS) intersects the parabola at point P, then
View Solution
