Find the intervals of the values of a for which the line y+x=0 bisects two chords drawn from the point (1+√2a2,1−√2a2) to the circle 2x2+2y2−(1+√2a)x−(1−√2a)=0Solution in Tamil

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Given, 2x2+2y2−(1+√23a)x−(1−√2a)y=0
⇒x2+y2−(1+√2a2)x−(1−√2a2)y=0
Since, y + x = 0 bisects two chords of this circle, mid points of the chords must be of the form (α,−α).
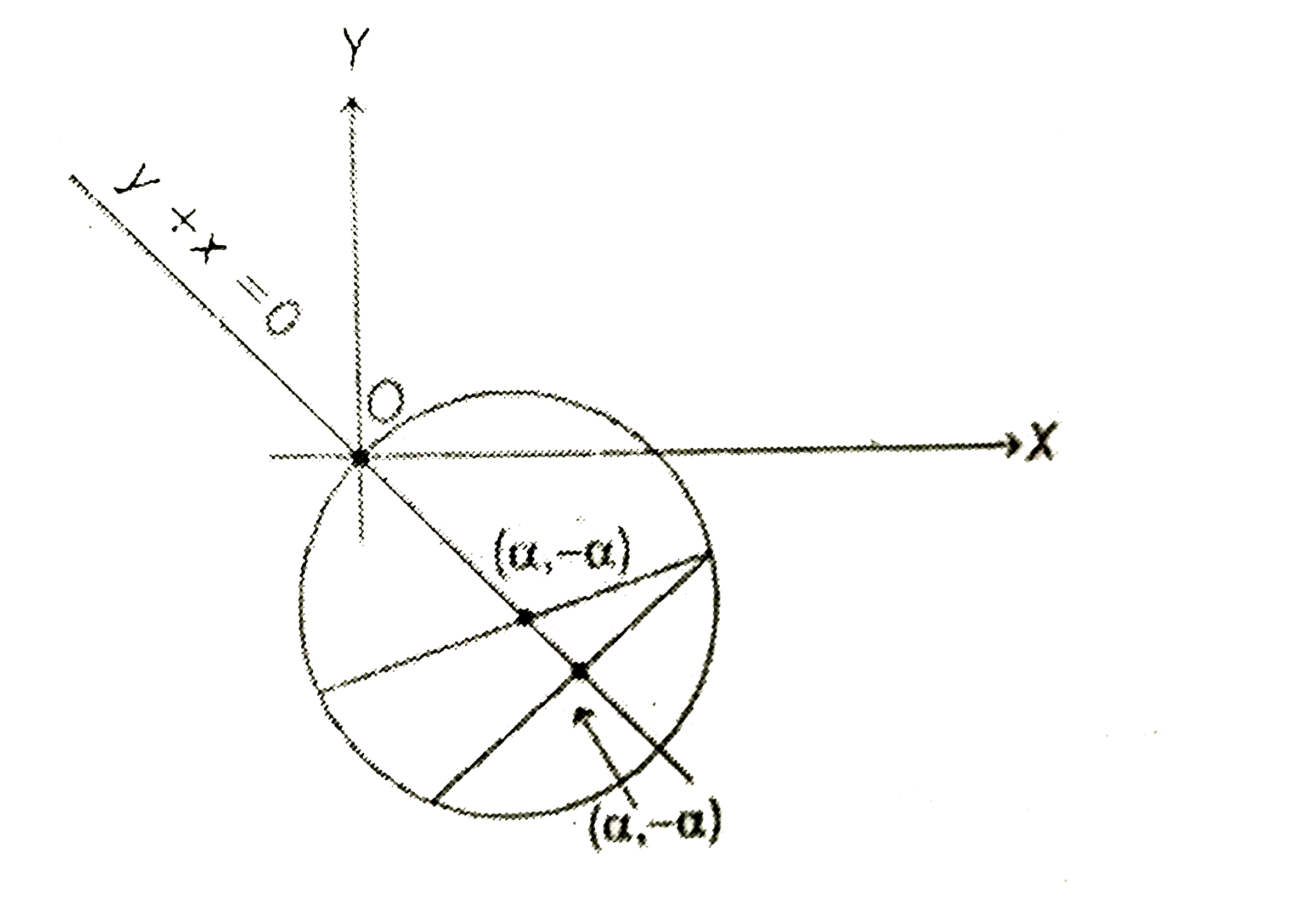
ocr_image
Equation of the chord having (α,−α) as mid point is
T=S1
⇒xα+y(−α)−(1+√2a4)(x+α)−(1−√2a4)(y−α)
a2+(−α)2−(1+√2a2)α−(1−√2a2)(−α)
⇒4xα−4yα−(1+√2α)x−(1+√2a)α
−(1−√2a)y+(1−√2a)α
4α2+4α2−(1+√2a)⋅2α+(1−√2a)⋅2α
⇒4ax−45ay−(1+√2a)x−(1−√2a)y
=8α2−(1+√2a)α+(1−√2a)α
But this chord will pass through the point (1+√2a2)f−4α(1−√2a2)−(1+√2a)(1+√2a)2
−(1−√2a)(1−√2a)2
=8α2−2√2aα
⇒2α[(1+√2a−1+√2a)]=8α2−2√2aα
⇒4√2α−12[2+2√2a)2]=8α2−2√2aα
[∴(a+b)2+(a−b)2=2a2+2b2]
⇒8α2−6√2α+1+2a2=0
But this quadratic equation will have two distinct roots, if
(6√2a)2−4(8)(1+2a2)>0
⇒72a2−32(1+2a2)>0
⇒8a2−32>0
⇒a2−4>0
⇒a<−2∪a>2
Therefore, a∈(−∞,−2)∪(2,∞).

|