about to only mathematics Solution in Tamil
Video Solution
Text Solution
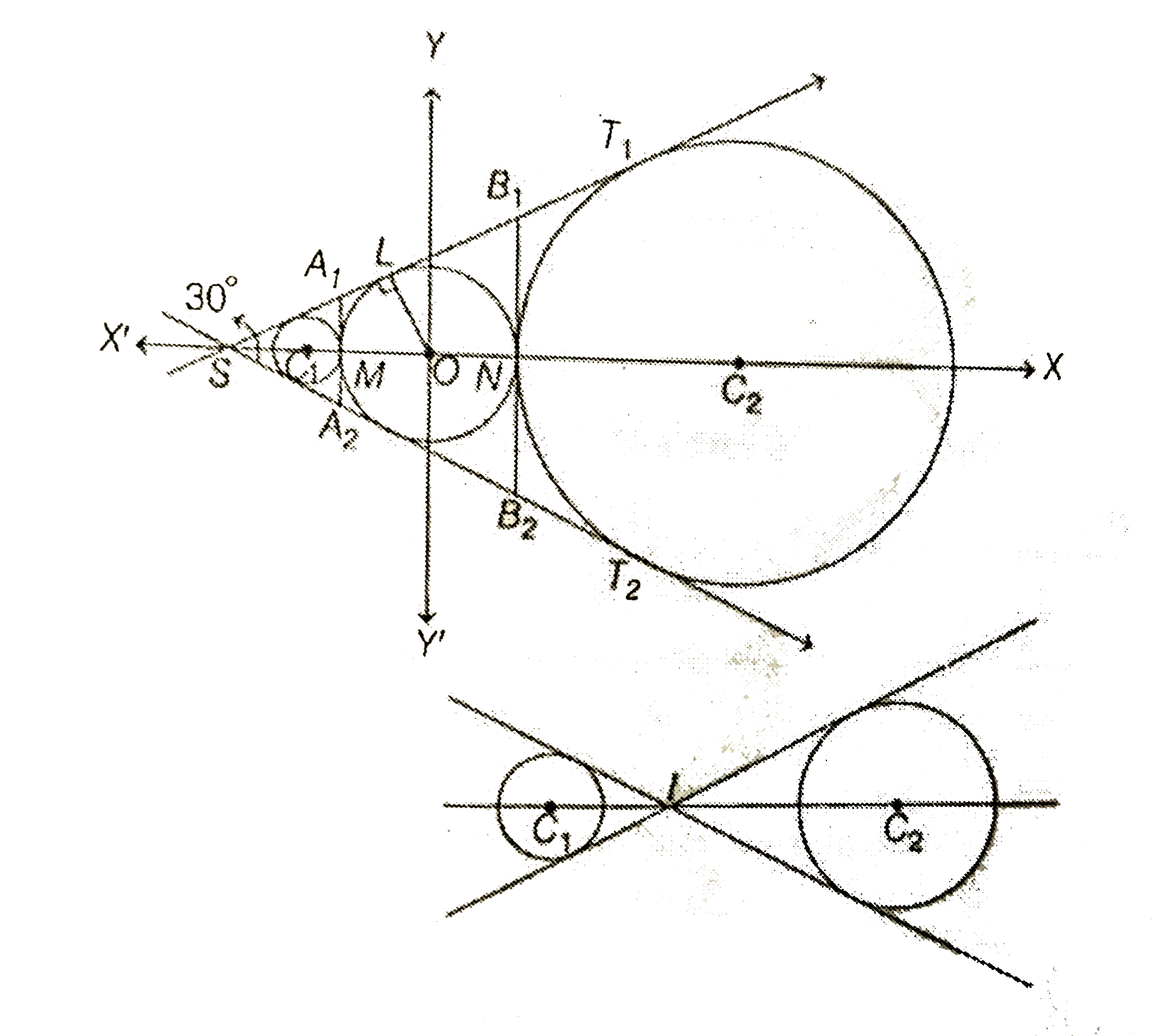
From figure it is clear that, ΔOLS is clear that, ΔOLS is a right triangle with right angle at L.
Also, OL = 1 and OS = 2
∴1sin(∠LSO)=12⇒∠LSO=30∘
Since,SA1=S2,ΔSA1A2 is an equilateral triangle.
the circle with centre at C1 is a circle insribed in the ΔSA1A2. Therefore centre C1 is a circle inscribed of ΔSA1A2. This C1 divides SM in the ratio 2:1. therefore coordinates of C1 are (−4/3,0) and its radius =C1M=1/3
∴ Its equation is (x+4/3)2+y2=(1/3)2 ...(i)
The other cirlce touches the equilateral triangle SB1A2.
externally. Its radius r is given by r=Δs−a
where B1B2=aButΔ=12)(a)(SN)=32a
and s−a=32a−a=a2
Thus, r = 3
⇒ Coordinates of C2 are (4,0).
∴ Equation of circle with centre at C2 is
(x−4)2+y2=32 ...(ii)
EQuation of common tangents to circle (i) and circle C are
x=−1andy=±1√3(x+2) [T1andT2]
Equation of common tangents to circle (ii) and circle C are
x=1andy=±1√3(x+2) ...[T1andT2]
Two tangents common to (i) and (ii) ar T1andT2 at O. To find the remaining two trasnverse tangents to (i) and (ii), we find a point I which divides the joint of C1C2 in the ratio r1:r2=1/3:3=1:9
Therefore, coordintates of I are (−4/5,0)
Equation of any line through I is y=m(x+4/5). It will touch (i) if
∣∣m(−43+45)−0∣∣√1+m2=13⇒∣∣∣−8m15∣∣∣=13√1+m2
⇒64m2=25(1+m2)
⇒39m2=25⇒m=±5√39
Therefore, these tangents are y=±5√39(x+45)
|
Similar Questions
about to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View SolutionWhich of the following statements is not correct about assignments in Mathematics?
View SolutionLearning Mathematics at upper primary level is about
View SolutionLearning mathematics at upper primary level is about
View Solution
