The locus of the middle point of the chord of contact of tangents drawn from points lying on the straight line 4x - 5y = 20 to the circle $x^{2} + y^{2} = 9$ is Solution in Tamil

A

$20 (x^{2} + y^{2}) - 36 x + 45 y = 0$

B

$20 (x^{2} + y^{2}) + 36 x - 45 y = 0$

C

$36 (x^{2} + y^{2}) - 20 x + 45 y = 0$

D

$36 (x^{2} + y^{2}) + 20 x - 45 y = 0$

Video Solution

Text Solution

Verified by Experts

PLAN If $S : a x^{2} + 2 h x y + b y^{2} + 2 g x + 2 f y + c$
then equation of chord bisected at $P (x_{1}, y_{1}) is T = S_{1}$
or ${axx}_{1} + h (x y_{1} + y x_{1}) + b y y_{1} + g (x + x_{1}) + f (y + y_{1}) + C$
$= a x_{1}^{2} + 2 h x_{1} y_{1} + b y_{1}^{2} + 2 g x_{1} + 2 f y_{1} + C$
Description of Situation As equation of chord of contact is $T = 0$

Here, equation of chord of contact w.r.t. P is
$x λ + y \cdot \frac{(4 λ - 20)}{5} = 9$
$5 λ x + (4 λ - 20) y = 45 ... (i)$

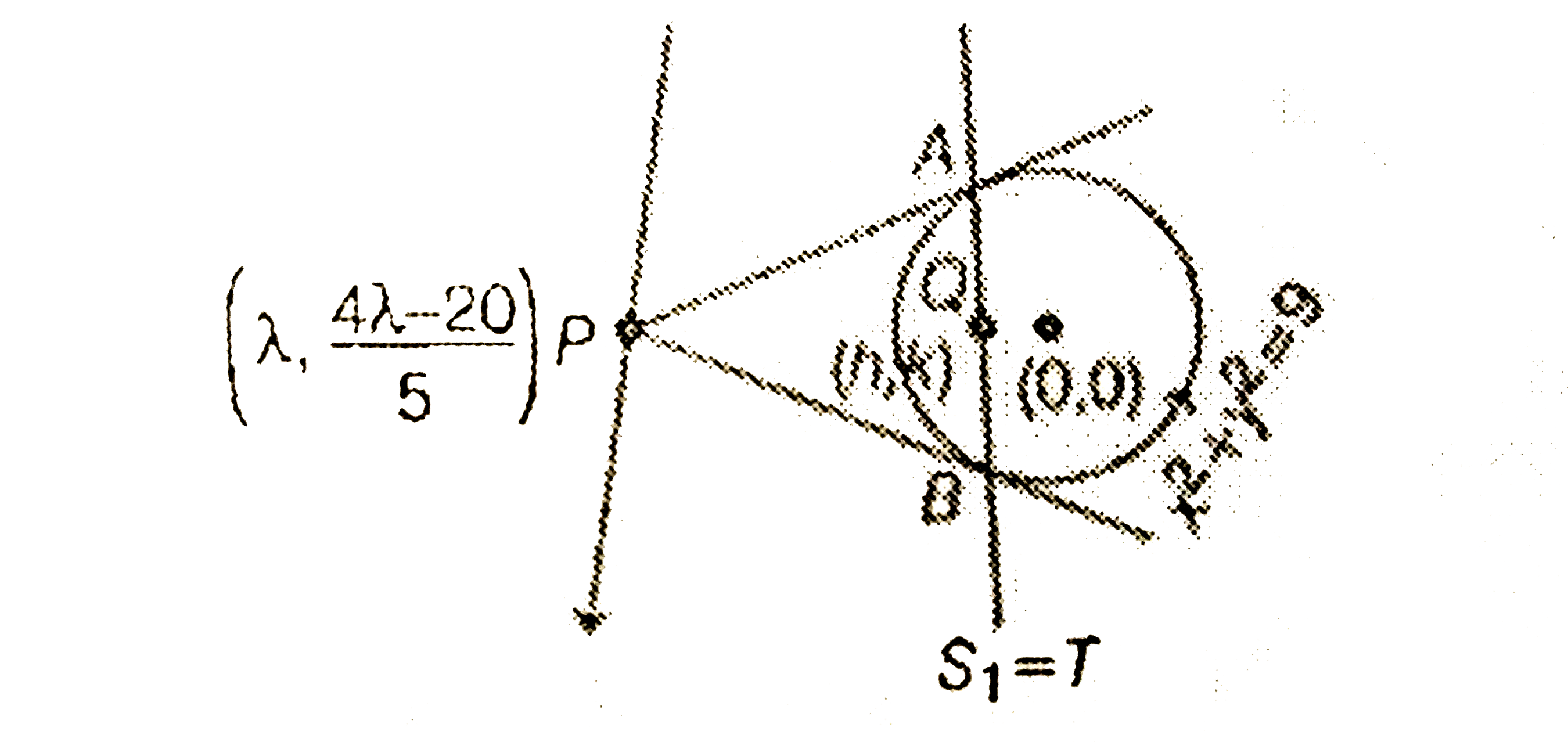
and equation of chord bisected at the point $Q (h, k)$ is
$x h + y k - 9 = h^{2} + k^{2} - 9$
$\Rightarrow x h + k y = h^{2} + k^{2} ... (i i)$
From Eqs. (i) and (ii) we get
$\frac{5 λ}{h} = \frac{4 λ - 20}{k} = \frac{45}{h^{2} + k^{2}}$
$∴ λ = \frac{20 h}{4 h - 5 k} and λ = \frac{9 h}{h^{2} + k^{2}}$
$\Rightarrow \frac{20 h}{4 h - 5 k} = \frac{9 h}{h^{2} + k^{2}}$
or $20 (h^{2} + k^{2}) = 9 (4 h - 5 k)$
or $20 (x^{2} + y^{2}) = 36 x - 45 y$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile