If two distinct chords, drawn from the point (p, q) on the circle x2+y2=px+qy (where pq≠q) are bisected by the x-axis, then (a)p2=q2 (b) p2=8q2 (c)p2<8q2 (d) p2>8q2Solution in Tamil
P2=q20
P^(2)=8q^(2)
P^(2)lt8q^(2)
P2>8q2
The correct Answer is:D
NOTE In soving a line and a circle there oftengenerate a quadratic equation and further we have to apply condition of Discrominant so equation convert from coordinate to quadratic equation.
From equation of circle it is clear that circle passes through origin. Let AB is chord of the circle.
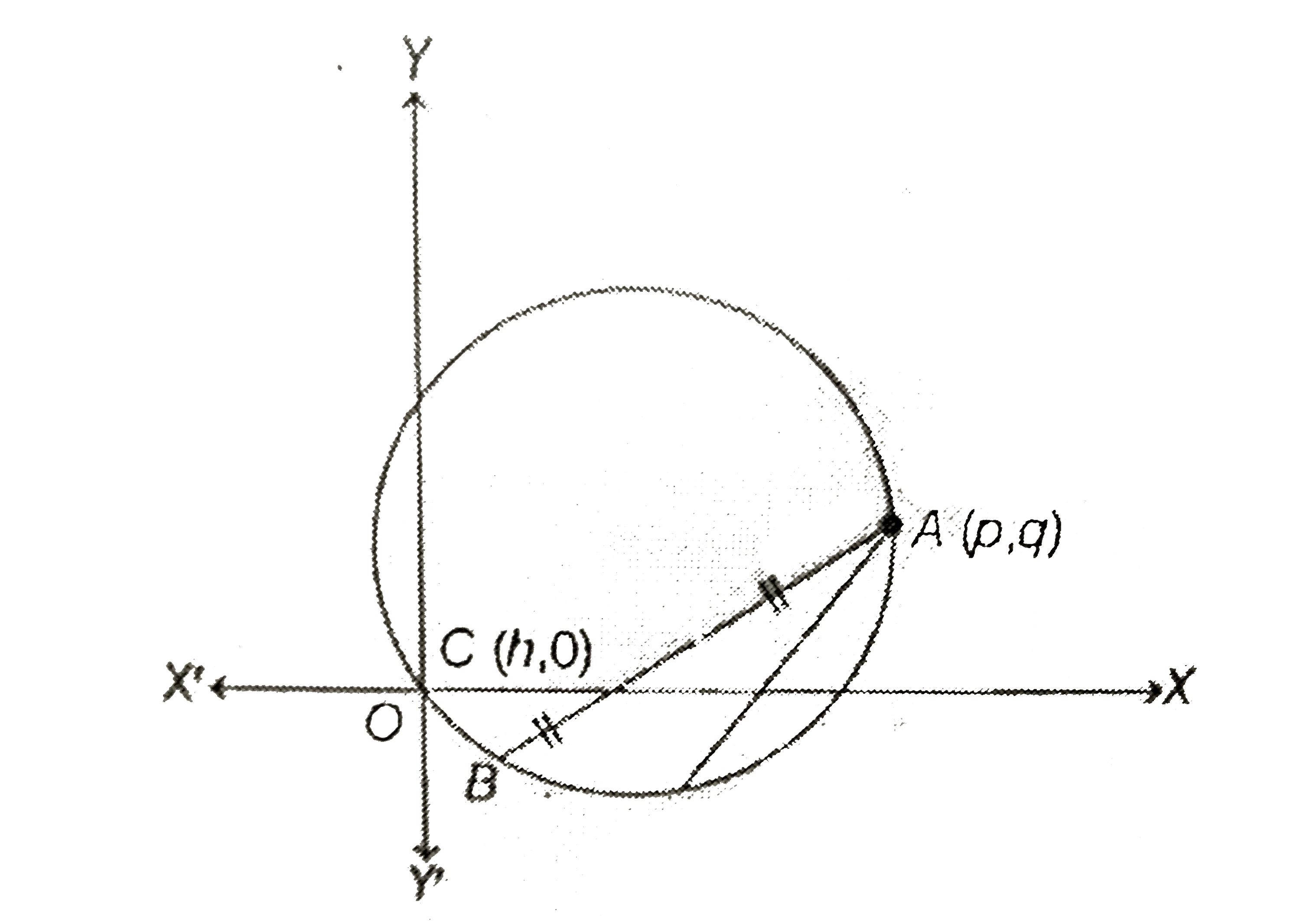
A≡(p,q)⋅C is mid-point and coordinate of C is (h, 0)
Then, coordinates of B are (−p+2h)2+(−q)2+P(−P+2h)+q(−q)
⇒p2+4h2−4ph+q2=−p2+2ph−q2
⇒2p2+2q2−6ph+4h2=0
⇒2h2−3ph+p2+q2=0 ...(i)
There ar given two distinct chords which are bisected at X- axis then, there will be two distinct value of h satisfying Eq. (i).
So, discriminant of this quardratic equation must be >0.
⇒D>0
⇒(−3p)2−4⋅2(p2+q2)>0
⇒9p2−8p2−8q2>0
⇒p2−8q2>0⇒p2>8q2
Similar Questions
यदि p तथा q भिन्न वास्तविक संख्याये है, तो 2{(x−p)(x−q)+(p−x)(p−q)+(q−x)(q−p)}=(p−q)2+(x−p)2+(x−q)2 सन्तुष्ट होगी
View SolutionIf AM and GM of x and y are in the ratio p: q, then x: y is : a)p−√p2+q2:p+√p2+q2 b) p+√p2−q2:p−√p2−q2 c)p:q d)p+√p2+q2:p−√p2+q2
View SolutionIf two distinct chords, drawn from the point (p, q) on the circle x^2+y^2=p x+q y (where p q!=q) are bisected by the x-axis, then p^2=q^2 (b) p^2=8q^2 p^2 8q^2
View SolutionIf sec αandα are the roots of x2−px+q=0, then (a) p2=q(q−2) (b) p2=q(q+2) (c)p2q2=2q (d) none of these
View SolutionIf two distinct chords, drawn from the point (p, q) on the circle x^2+y^2=p x+q y (where p q!=q) are bisected by the x-axis, then (a) p^2=q^2 (b) p^2=8q^2 (c) p^2 8q^2
View SolutionThe base BC of a ABC is bisected at the point (p,q) & the equation to the side AB&AC are px+qy=1 & qx+py=1 . The equation of the median through A is: (a) (p−2q)x+(q−2p)y+1=0 (b) (p+q)(x+y)−2=0 (c) (2pq−1)(px+qy−1)=(p2+q2−1)(qx+py−1) (d)none of these
View SolutionIf sec alpha and alpha are the roots of x^2-p x+q=0, then (a) p^2=q(q-2) (b) p^2=q(q+2) (c) p^2q^2=2q (d) none of these
View SolutionIf two distinct chords, drawn from the point (p, q) on the circle x^2+y^2=p x+q y (where p q!=q) are bisected by the x-axis, then (a) p^2=q^2 (b) p^2=8q^2 p^2 8q^2
View Solution
