The straight line x+2y=1 meets the coordinate axes at A and B. A circle is drawn through A, B and the origin. Then the sum of perpendicular distances from A and B on the tangent to the circle at the origin is Solution in Tamil

A

$2 \sqrt{5}$

B

$\frac{\sqrt{5}}{4}$

C

$4 \sqrt{5}$

D

$\frac{\sqrt{5}}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

According to given information, we have the following figure.

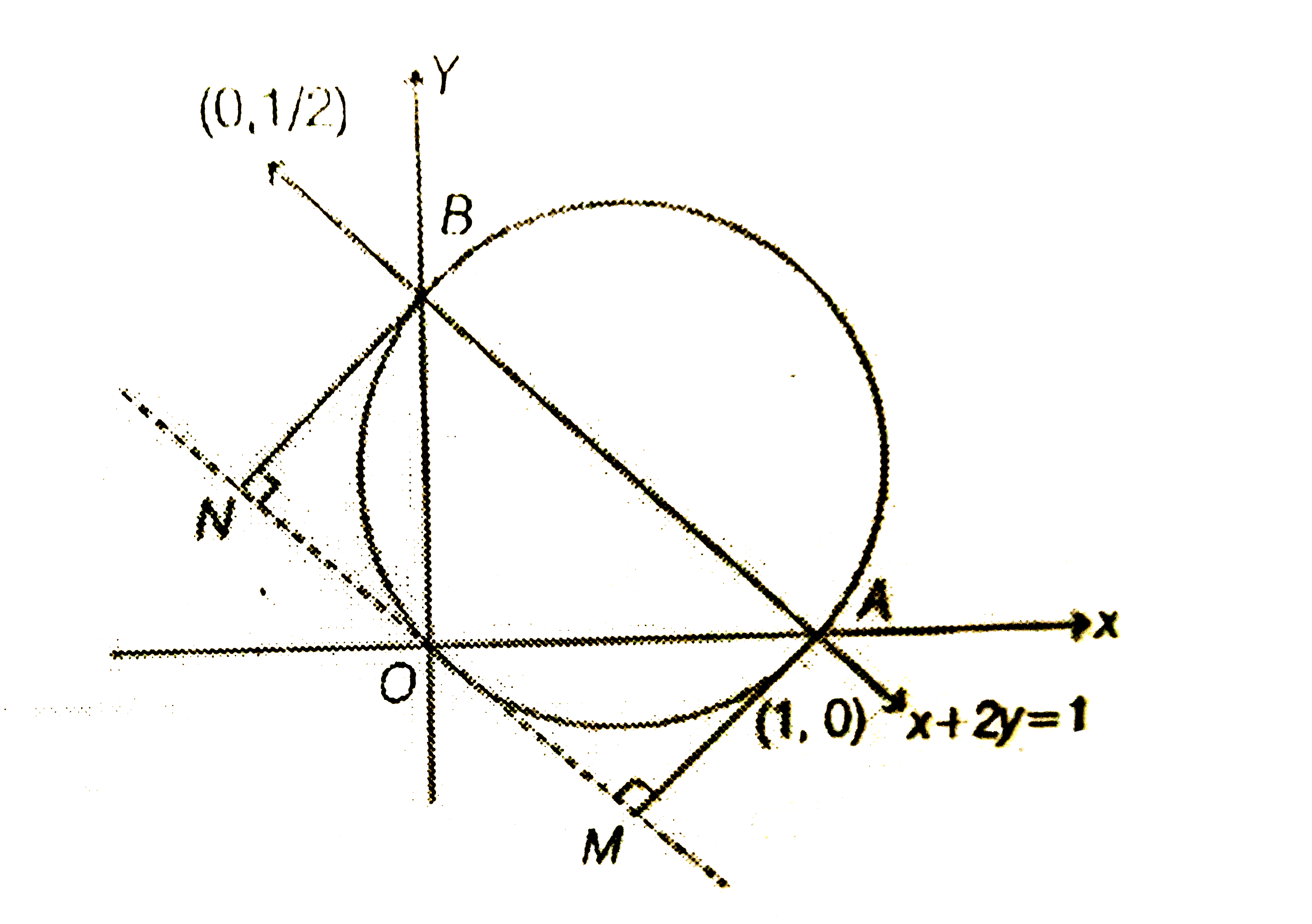
From figure, equation of circle (diameter form) is
$(x - 1) (x - 0) + (y - 0) ((y - \frac{1}{2}) = 0$
$\Rightarrow x^{2} + y^{2} - x - \frac{y}{2} = 0$
Equation of tangent at (0, 0) is $x + (y) + (2) = 0$
$[∴ equation of tangent at (x_{1}, y_{1}) is given by T = 0 Here, T = 0$
$\Rightarrow {xx}_{1} + y y_{1} - \frac{1}{2} (x + x_{1}) - \frac{1}{4} (y + y_{1}) = 0]$
$\Rightarrow 2 x + y = 0$
Now, $A M = \frac{| 2.1 + 1.0 |}{\sqrt{5}} = \frac{2}{\sqrt{5}}$
$[∴ distance of a point P (x_{1}, y_{1})$ from a line
$a x + b y + c = 0 is \frac{| a x_{1} + b y_{1} + c |}{\sqrt{a^{2} + b^{2}}}]$
and $B N = \frac{∣ ∣ 2.0 + 1 (\frac{1}{2}) ∣ ∣}{\sqrt{5}} = \frac{1}{2 \sqrt{5}}$
$∴ A M + B N = \frac{2}{\sqrt{5}} + \frac{1}{2 \sqrt{5}} = \frac{4 + 1}{2 \sqrt{5}} = \frac{\sqrt{5}}{2}$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile