about to only mathematics Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $16 : 1$

Suppose the circle have centres at $C_{1}, C_{2} and C_{3}$ with Radius $R_{1}, R_{2} and R_{3}$ respectively.Let the circle touch at A,B and C. Let the common tangents at A,B and C meet at O. We have OA = Ob = OC = 4 [given] Now, the circle with centre at O and passing through A, B and C is the incircle of the triangle $C_{1} C_{2} C_{3}$ (because $O A ⊥ C_{1} C_{2}$ ).
Therefore, the inradius of $Δ C_{1} C_{2} C_{3}$ is 4 .
and $r = \frac{Δ}{s} ... (i)$

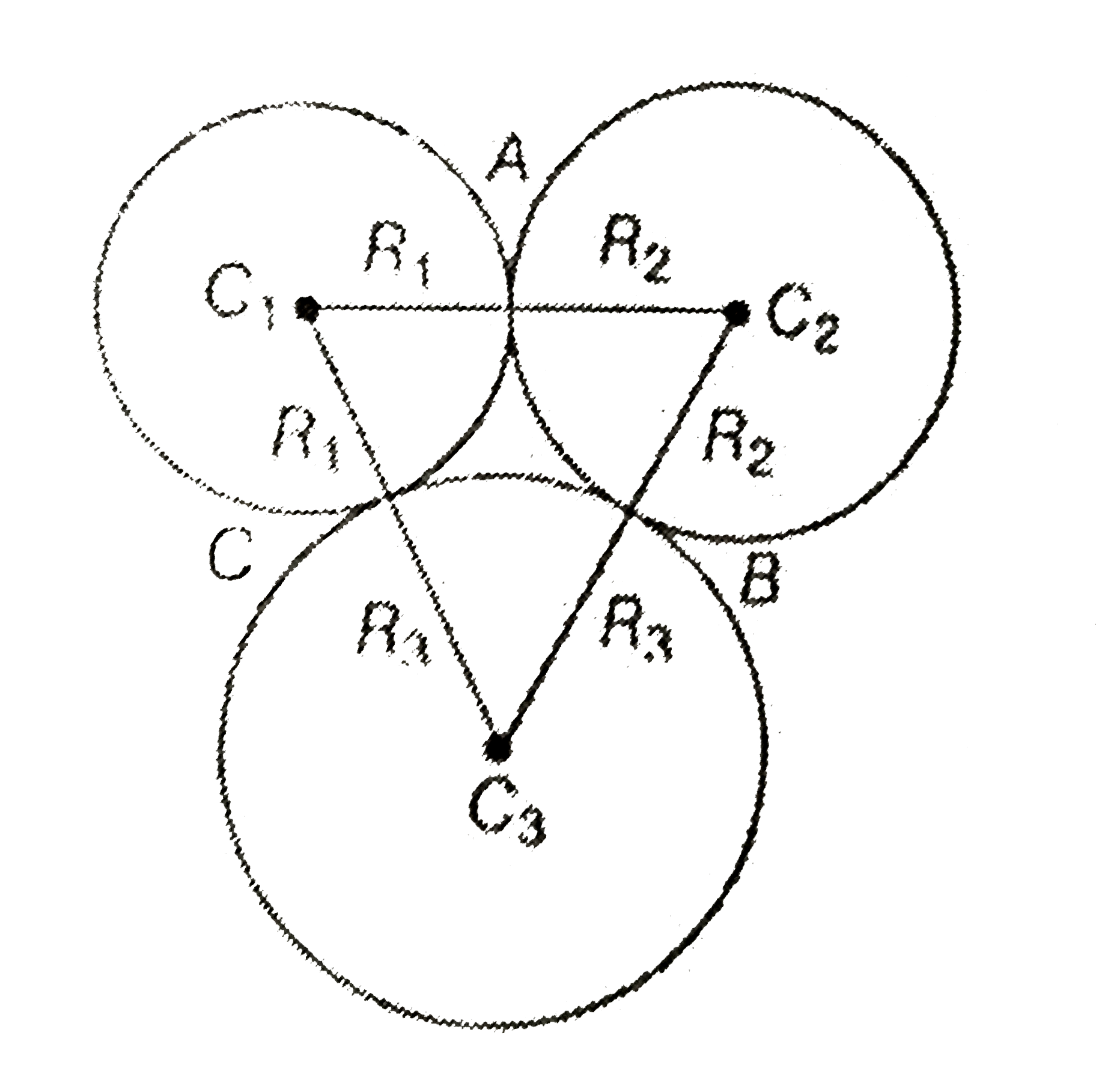
Nowm perimeter of a triangle
$2 s = R_{1} + R_{2} + R_{2} + R_{3} + R_{3} + R_{1}$
$\Rightarrow 2 s = 2 (R_{1} + R_{2} + R_{3})$
$\Rightarrow s = R_{1} + R_{2} + R_{3}$
and $Δ = \sqrt{s (s - a) (s - b) (s - c)}$
$= \sqrt{(R_{1} + R_{2} + R_{3}) (R_{3}) (R_{2}) (R_{1})}$
From Eq. (i), $4 = \frac{\sqrt{(R_{1} R_{2} R_{3}) (R_{1} + R_{2} + R_{3})}}{R_{1} + R_{2} + R_{3}}$
$\Rightarrow 16 = \frac{\sqrt{R_{1} R_{2} R_{3} (R_{1} + R_{2} + R_{3})}}{R_{1} + R_{2} + R_{3}}$
$\Rightarrow 16 = \frac{R_{1} R_{2} R_{3}}{R_{1} + R_{2} + R_{3}}$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile