A particle starts from a point z0=1+i where i=√−1. lt moves horizontally away from origin by 2 units and then vertically away from origin by 3 units to reach a point z1, From z1 particle moves √5 units in the direction of 2ˆi+3ˆj and then it moves through à n angle of cosec−12 in anticlockwise direction of a circle with centre at origin to reach a point z2. The arg z1 is given bySolution in Tamil
6+7i
−7+6i
7+6i
−6+7i
The correct Answer is:D
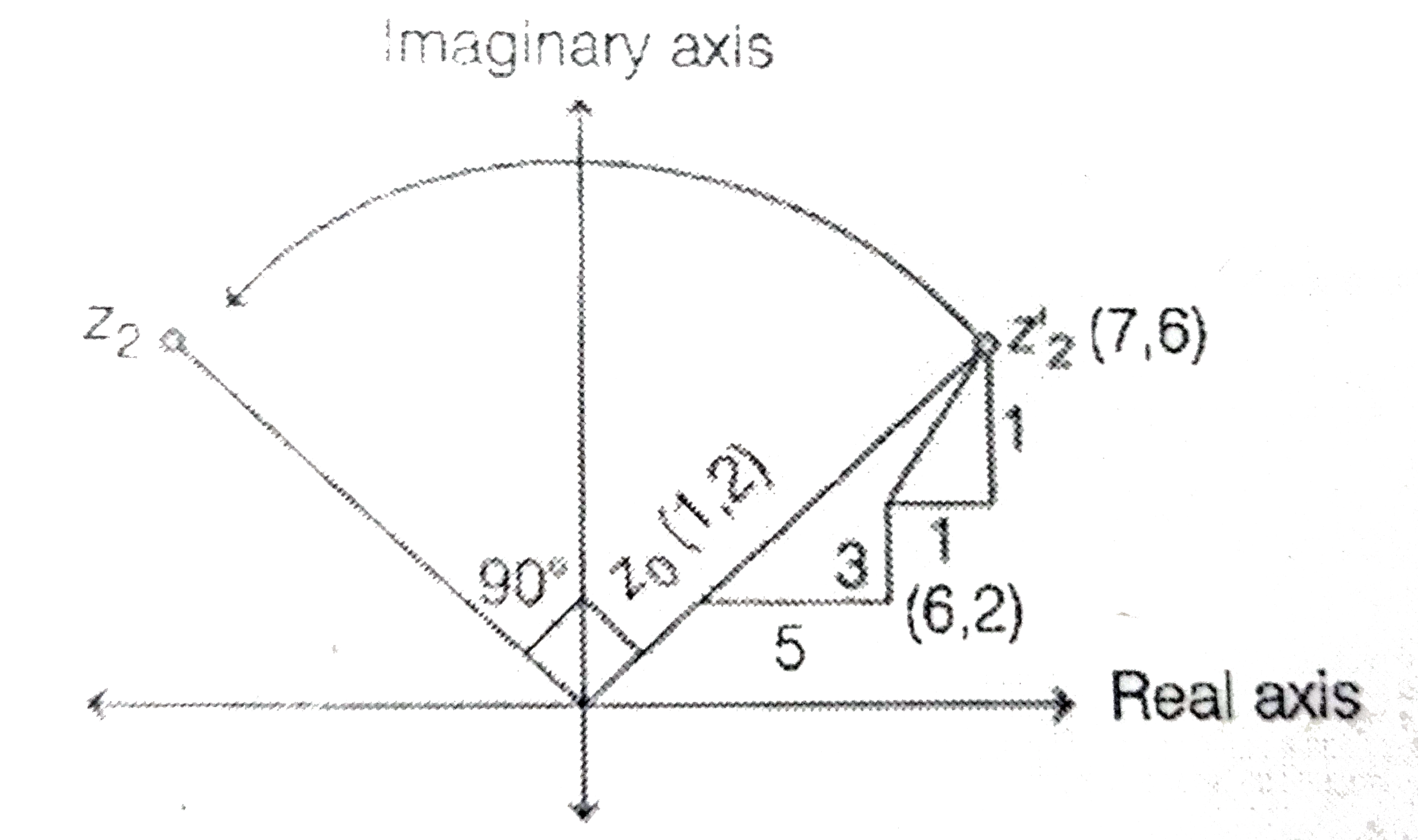
z2=(6+√2cos45∘,5+√2sin45∘) = (7,6)= 7 + 6i By rotaion about (0,0)
z2z2=eIπ/2⇒z2=z2(eiπ2)
=(7+6i)(cosπ2+isinπ2)=(7+6i)(i)=−6+7i
Similar Questions
Let A(z1)andB(z2) be lying on the curve |z−3−4i|=5, where |z1| is maximum. Now, A(z1) is rotated about the origin in anticlockwise direction through 90∘ reaching at P(z0). If A,BandP are collinear then the value of (|z0−z1|⋅|z0−z2|) is _______.
View Solutionएक कण P बिंदु z0=1+2i जहां i=√−1 से चलना प्रारंभ करता है। यह पहले क्षैतिज दिशा में 5 एकांक मूलबिंदु से दूरी की ओर व फिर ऊर्ध्व दिशा में 3 एकांक मूलबिंदु से दूर की ओर चल कर बिंदु z1 पर पहुंचता है। बिंदु z1 से यह कण सदिश ˆi+ˆj की दिशा में √2 एकांक चलता है व फिर ऊर्ध्व दिशा में 3 एकांक मूलबिंदु से दूरी की ओर चल कर बिंदु z1 पर पहुंचता है। बिंदु z1 से यह कण सदिश ˆi+ˆj की दिशा में √2 एकांक चलता है व फिर यह एक वृत्त, जिसका केंद्र मूलबिंदु है पर वामावर्त π2 कोण चलकर बिंदु z2 पर पहुंचता है। बिंदु z2 निम्न है।
View SolutionIf d.c's of the line joining the origin and a point unit distance from the origin are 1√3,1−(2),λ then the point is
View Solutionएक कण बिन्दु z0=1+i से गति करना प्रारम्भ करता है जहाँ i=√−1 यह मूल बिन्दु से क्षेतिज दिशा में 2 मात्रक दूर व उर्ध्वाधर दिशा में 3 मात्रक दूर बिन्दु z1 तक पहुँचता है, बिन्दु z1 से कण √5 मात्रक गति करता है तथा 2ˆi+ˆj दिशा में चलता है तत्पश्चात् यह वामावर्त्त दिशा में एक वृत्ताकार पथ पर कोण cosec−1√2 तय करता है तथा बिन्दु z2 तक पहुँचता है। यदि वृत्त का केन्द्र मूल बिन्दु है तो कोणांक z2 का मान है
View Solutionएक कण P बिन्दु z0=1+2i से शुरू होता है, जहाँ i=√−1 है। यदि वह पहले मूल बिन्दु से विपरित क्षैतिज दिशा में 5 इकाई तथा इसके बाद मूल बिन्दु से विपरीत उर्ध्वाधर दिशा में 3 इकाई जाता है तो बिन्दु z1 पर पहुंचता है। z1 से सदिश ˆi+ˆj की दिशा में कण √2 इकाई दूरी तय करता है। तत्पश्चात् कण मूल बिन्दु को केन्द्र मानते हुये वामावृत दिशा में π2 से घूर्णन करके z2 पर पहुचता है। बिन्दु z2 है
View SolutionO is the origin and P is point at a distance of 3 units from origin. If direction ratios of OP are <1,−2,−2>, then the coordinates of P are
View Solution(3, b) বিন্দুটি মূলবিন্দু থেকে 5 একক দূরত্বে থাকলে b-এর মান হবে –
View SolutionA particle P starts from the point z_0=1+2i , where i=sqrt(-1) . It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point z_1dot From z_1 the particle moves sqrt(2) units in the direction of the vector hat i+ hat j and then it moves through an angle pi/2 in anticlockwise direction on a circle with centre at origin, to reach a point z_2dot The point z_2 is given by (a) 6+7i (b) -7+6i (c) 7+6i (d) -6+7i
View Solution