Let and If is any complex number such that the argument of is then prove that .Solution in Tamil
Since
and arg represente lecue of z is a circle shown as form the figure whose center is (7,y) and clearly OC = 9 OD = 6 + 3 =9
Center = (7,9) and readius
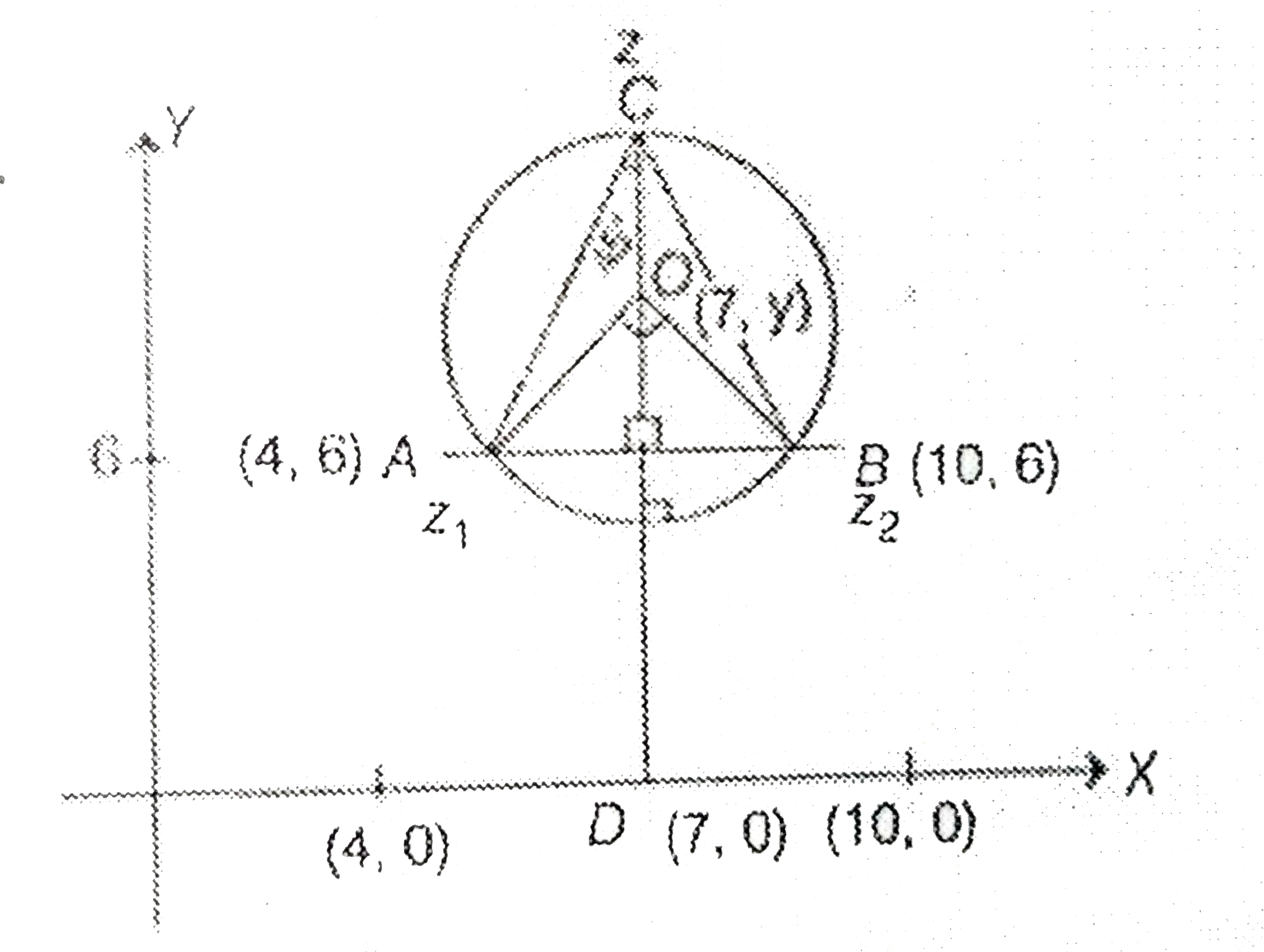
Equation of circle is
Similar Questions
If arg z−z1z2−z1 = 0 for three distinct complex numbers z,z1,z2 then the three points are
03:17View Solutionlet z1=10+6i and z2=4+6i if z is nay complex number such that argument of z−z1z−z2 is π4 the prove that |z−7−9i|=3√2
07:46View SolutionIf z1=10+6iandz2=4+2i be two complex numbers and z be a complex number such that arg(z−z1z−z2)=π4 , then locus of z is an arc of a circle whose
(a) centre is 5+7i
(b) centre is 7+5i
(c) radius is √26
(d) radius is √1306:30View SolutionThe maximum area of the triangle formed by the complex coordinates z,z1,z2 which satisfy the relations |z−z1|=|z−z2| and ∣∣∣z−z1+z22∣∣∣≤r,where r>|z1−z2| is
11:49View SolutionLet z1 and z2 be two distinct complex numbers and let z=(1−t)z1+tz2 for some real number t with 0<t<1. If arg(w) denotes the principal argument of a nonzero complex number w , then which of the following is/are correct
(a) |z−z1|+|z−z2|=|z1−z2|
(b) arg(z−z1)=arg(z−z2)
(c) (z−z1)¯¯¯¯¯¯¯¯¯¯¯¯z2−z1=¯¯¯¯¯¯¯¯¯¯z−z1(z2−z1)
(d) arg(z−z1)=arg(z2−z1).06:33View SolutionLet z1=10+6i and z2=4+6t If z is any complex number such that the argument of (z−z1)(z−z2) is π4, then prove that |z−7−9i|=3√2 .
03:29View SolutionIf z1andz2 both satisfy the relation z+¯z=2|z−1|andarg(z1−z2)=π4, then Im(z1+z2) equals
04:12View SolutionThe maximum area of the triangle formed by the complex coordinates z, z_1,z_2 which satisfy the relations |z-z_1|=|z-z_2| and |z-(z_1+z_2 )/2| |z_1-z_2| is
05:23View Solution
