Let z1 and z2
be two distinct complex numbers and let z=(1−t)z1+tz2
for some real number t
with 0<t<1.
If arg(w)
denotes the principal argument of a nonzero complex number w
, then which of the following is/are correct
(a) |z−z1|+|z−z2|=|z1−z2|
(b) arg(z−z1)=arg(z−z2)
(c) (z−z1)¯¯¯¯¯¯¯¯¯¯¯¯z2−z1=¯¯¯¯¯¯¯¯¯¯z−z1(z2−z1)
(d) arg(z−z1)=arg(z2−z1).Solution in Tamil
The correct Answer is:a,c,d
Given z=(1−t)z1+jtz2(1−t)+t
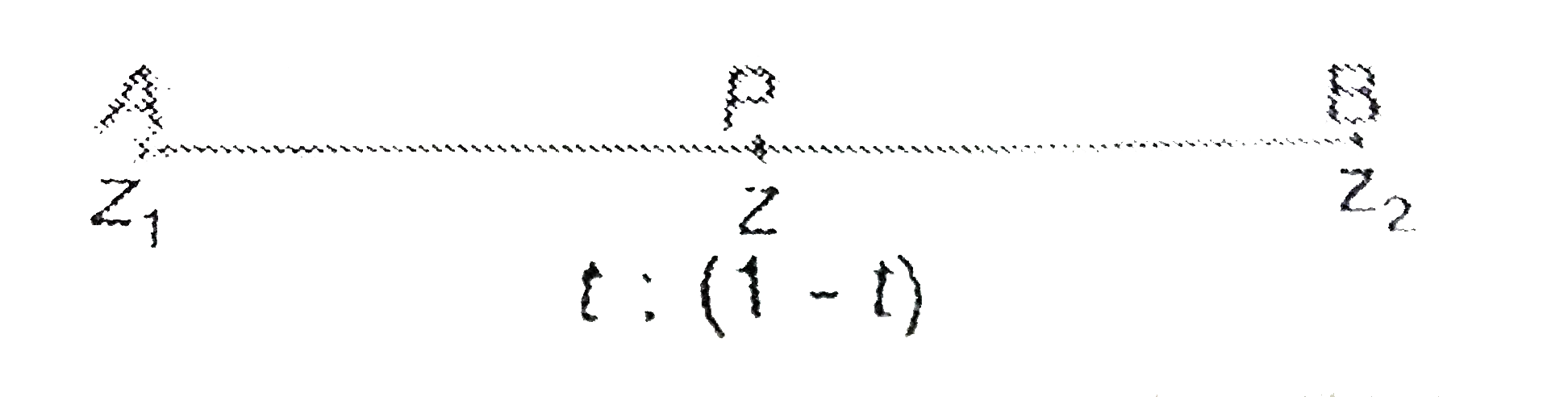
Clearly z divides z1 and z2 in the ratio of t:(1−t),0<t<1
⇒AP+BP=ABie|z−z1|+|z+z2|=|z1−z2|
⇒ option (a) is true
Also arg(z−z1)=arg(z2−z1)
⇒arg((z−z1)(z2−z1))=0
∴zz_1z2−z1 is purely real .
⇒z−z1z2−z1=¯z−z1z2−¯z1
or ∣∣∣z−z1 ¯z−¯z1z2−z1 ¯z2−¯z1∣∣∣=0
Option (c ) is correct
Similar Questions
Let z1andz2 be two distinct complex numbers and let z=(1−t)z1+tz2 for some real number t with 0<t<1. If a r g(w) denotes the principal argument of a nonzero complex number w , then
|z−z1|+|z−z2|=|z1−z2| (z−z1)=(z−z2)
∣∣z−z1z−(z)1z2−z1(z)2−(z)1∣∣=0
arg(z−z1)=arg(z2−z1)
View SolutionIf for complex numbers z1 and z2 ,arg(z1)−arg(z2)=0 , then show that |z1−z2|=||z1|−|z2∣∣
View SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|andarg(z1)+arg(z2)=π , then show that z1,=−(z)2.
View SolutionIf z1 and z2 are two nonzero complex numbers such that |z1−z2|=|z1|−|z2| then arg z1-argz2 is equal to
View SolutionIf arg z−z1z2−z1 = 0 for three distinct complex numbers z,z1,z2 then the three points are
View SolutionIf for the complex numbers z1 and z2, |z1+z2|=|z1−z2|, then Arg(z1)−Arg(z2) is equal to
View SolutionIf z1 and z2 are two complex number such that |z1|<1<|z2| then prove that ∣∣∣1−z1¯z2z1−z2∣∣∣<1
View SolutionLet z1 and z2 be two distinct complex numbers and let z=(1−t)z1+tz2 for some real number t with 0<t<1. If arg(w) denotes the principal argument of a nonzero complex number w , then which of the following is/are correct
(a) |z−z1|+|z−z2|=|z1−z2|
(b) arg(z−z1)=arg(z−z2)
(c) (z−z1)¯¯¯¯¯¯¯¯¯¯¯¯z2−z1=¯¯¯¯¯¯¯¯¯¯z−z1(z2−z1)
(d) arg(z−z1)=arg(z2−z1).
View Solution
