Let
A={0∈(−π2,π):3+2isinθ1−2isinθ is purely imaginary}
Then the sum of the elements in A isSolution in Tamil
A
3π4
B
5π6
C
π
D
2π3
Video Solution
Text Solution
The correct Answer is:A
Let z=(3+2isinθ1−2isinθ)×(1+2Isinθ1+2Isinθ)
(reationaliisng the denomunator)
=3−4sin2θ+8Isinθ1+4sin2θi
As z is purely imaginary , so real part of z=0
∴3−4sin2θ1+4sin2θ=0⇒3−4sin2thet=0
⇒sin2θ=34⇒sinθ=±√32
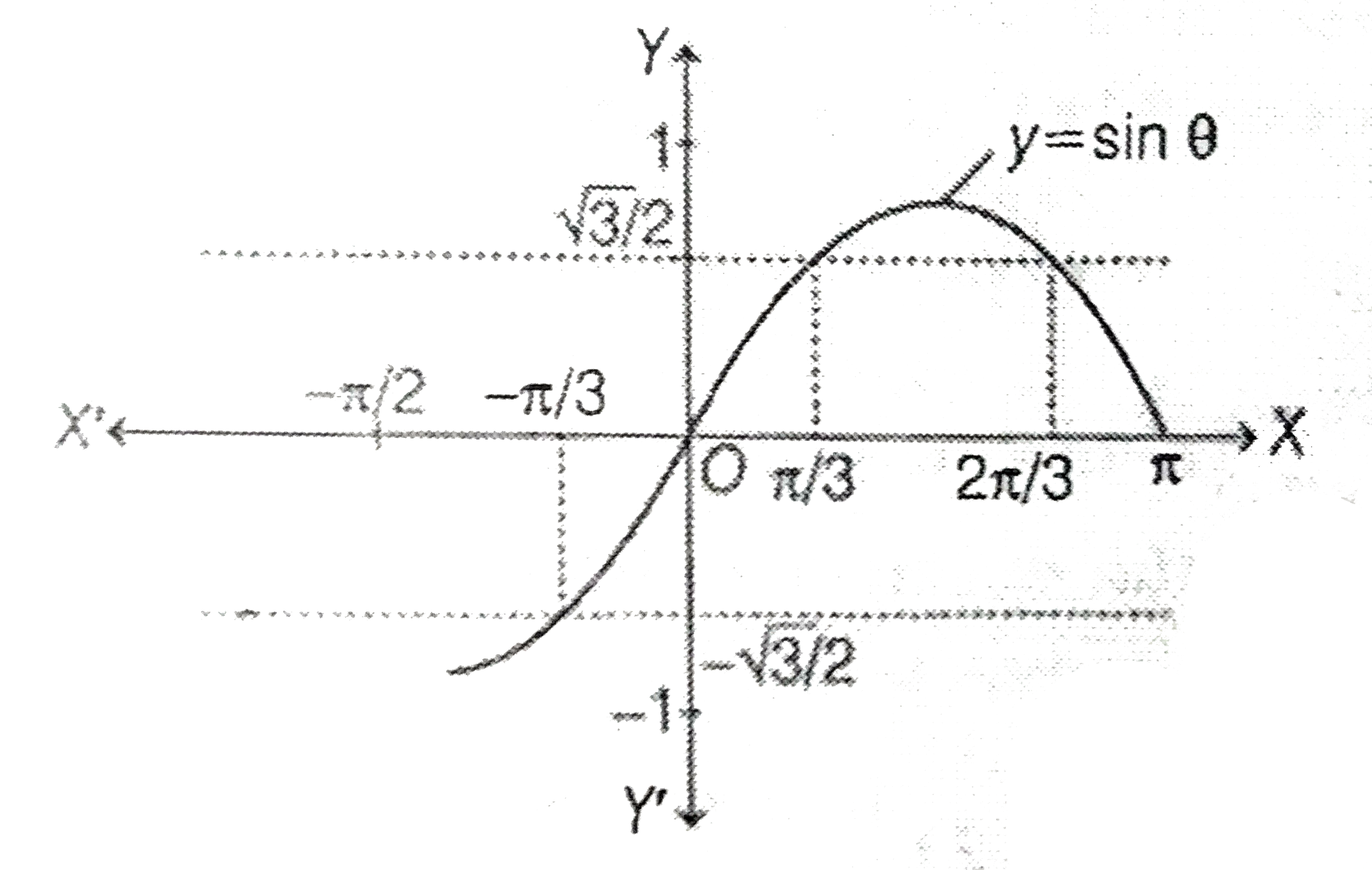
⇒θ≠{−π3,π3,2π3}
Sum of values of θ=2π3
|
Similar Questions
Find the real values of θ when 3+2isinθ1−2isinθ will be
purely imaginary.
View SolutionFind the theta such that (3+2i sin theta)/(1-2 isin theta) is (a) real (b) purely imaginary
View Solutionमाना A={(θ∈(−π2,π):3+2isinθ1−2isinθ),(मात्र काल्पनिक है)} तो A के अवयवों का योग है
View SolutionFind real θ such that
3+2isinθ1−2isinθ is purely real.
View SolutionFind the real values of θ , such that 3+2isinθ1−2isinθ is purely
Real
View SolutionFind the real values of θ , such that 3+2isinθ1−2isinθ is purely
Imaginary
View SolutionFind real value of θ for which 3+2isinθ1−2isinθ is purely real.
View SolutionLet A={θ∈(−π2,π):3+2isinθ1−2isinθ is purely imaginary }
Then the sum of the elements in A is
View Solution
