A country has a food deficit of 10%. Its population grows continuously at a rate of 3% per year. Its annual food production every year is 4% more than that of the last year. Assuming that the average food requirement per person remains constant, prove that the country will become self-sufficient in food after n years, where n is the smallest integer bigger than or equal to ln10−ln9ln(1.04)−0.03Solution in Tamil
Let X0 be initial population of the country and Y0 be its
initial food production. Let the average consumption be
a unit. Therefore, food requird initially aX0. It is given
Yp=aX0(90100)=0.9aX0…(i)
Let X be the population of the country in year t.
Then, dXdt= Rate of change of population
=3100X=0.03X
⇒dXX=0.03dt⇒∫dXX=∫0.03dt
⇒logX=0.03t+c
⇒X=A⋅e0.03t,whereA=ec
Att=0,X=X0,thusX0=A
∴X=X0e0.03t
Let Y be the food production in year t.
Then, Y=Y0(1+4100)t=0.9aX0(1.04)t
∴Y0=0.9aX0 [from Eq. (i)]
Food consumption in the year t is aX0e0.03t.
Again, Y−X≥0 [given]
⇒0.9X0a(1.04)t>aX0e0.03t
⇒(1.04)te0.03t>10.9=109.
Taking log on both sides, we get
t[log(1.04)−0.03]≥log10−log9
⇒t≥log10−log9log(1.04)−0.03
Thus, The least integral values of the year n, when the
country becomes self-sufficient is the smallest integer
greater than or equal to log10−log9log(1.04)−0.03.
Similar Questions
প্রতিবছর জনসংখ্যা 10% বৃদ্ধি হলে, n বছর পর জনসংখ্যা হয় P। n বছর পূর্বে জনসংখ্যা কত ছিল?
View SolutionIf the rate of increase in population is r% per year, the population after n years is p, find the population that was n years before.
View SolutionA country has a food deficit of 10%. Its population ear. Its annual food production every year is 4% more than that of the last year Assuming that the average food requirement per person remains constant, prove that the country will become self-sufficient in food after n years, where n is the smallest integer bigger than or equal to loge10−loge9(loge1.04)−0.03
View SolutionA country has a food deficit of 10% . Its population grows continuously at a rate of 3% per year. Its annual food production every year is 4% more than that of the last year. Assuming that the average food requirement per person remains constant, prove that the country will become self-sufficient in food after n years, where n is the smallest integer bigger than or equal to (ln10-ln9)/(ln(1.04)-0.03)
View SolutionA country has a food deficit of 10%. Its population grows continuously at the rate of 3% per year. Its annual food production every year is 4% more than that of the last year Assuming that the average food requirement per person remains constant, prove that the country will become self-sufficient in food after n years, where n is the smallest integer bigger than or equal to loge10−loge9(loge1.04)−0.03
View SolutionA country has a food deficit of 10%. Its population grows continuously at the rate of 3% per year. Its annual food production every year is 4% more than that of the last year Assuming that the average food requirement per person remains constant, prove that the country will become self-sufficient in food after n years, where n is the smallest integer bigger than or equal to loge10−loge9(loge1.04)−0.03
View SolutionThe population of a village in the first year 5% and in the next two years 10% increased by. for some reason in the last year 4% decreased. If after a total of four years its population becomes 60984, then what was its population in the beginning?
View SolutionThe graph shows the production of food grains of a country in different years. Study the graph and answer the questions.
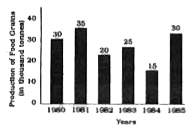
The sum of the production of food grains in the years 1982 and 1984 is equal to that in the year :
View Solution
