Consider a pyramid OPQRS located in the first octant (x≥0,y,z≤0)with O as origin and OP an OR along the z-axis and the y-axis , respectively , the base OPQR of the pyramid is a squre with OP=3. the point S is directly above the midpoint T of diagonal OQ such that TS=3, then Solution in Tamil
the acute angle between OQ and OS is π3
the equation of the plane containing the ΔOQS is x−y=0
the length of the perpendicular from P to the plane containing the ΔOQS is 3√2
the perpendicular distance from O to the straight line containing RS is √152
The correct Answer is:B, C, D
Given, square base OP=OR=3
∴ P(3,0,0),R=(0,3,0)
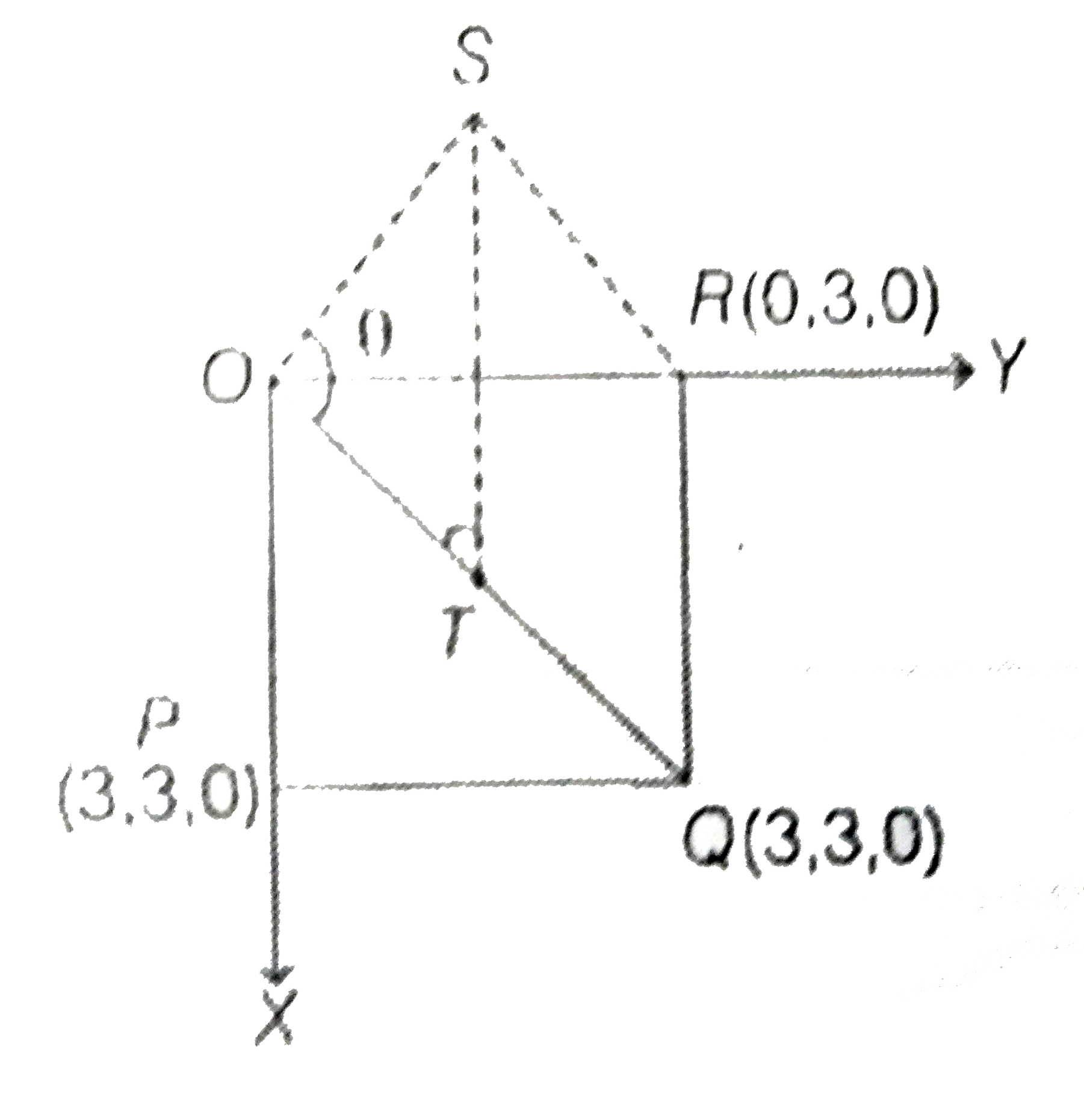
Also, mid-point of OQ is T(32,32,0).
Since, S is directly above the mid-point T of diagonal OQ and ST=3.
i.e. S(32,32,3)
Here, DR's of OQ(3,3,0) and DR's of OS(32,32,3).
∴cosθ=92+92√9+9+0√94+94+9=9√18.√272=1√3
∴ Option (a) is incorrect.
Now, equation of the plane containing the ΔOQS is
∣∣
∣
∣∣xyz3303/23/23∣∣
∣
∣∣=0⇒∣∣
∣
∣∣xyz110112∣∣
∣
∣∣=0
⇒ x(2−0)−y(2−0)+z(1−1)=0
⇒ 2x−2y=0 or x−y=0
∴ Option (b) is correct.
Now, length of the perpendicular from P(3,0,0) to the plane containing ΔOQS is |3−0|√1+1=3√2
∴ Option (c) is correct.
Here, equation of RS is
x−03/2=y−3−3/2=z−03=λ
⇒ x=32λ,y=−32λ+3,z=3λ
To find the distance from O(0,0,0) to RS.
Let M be the foot of perpendicular.
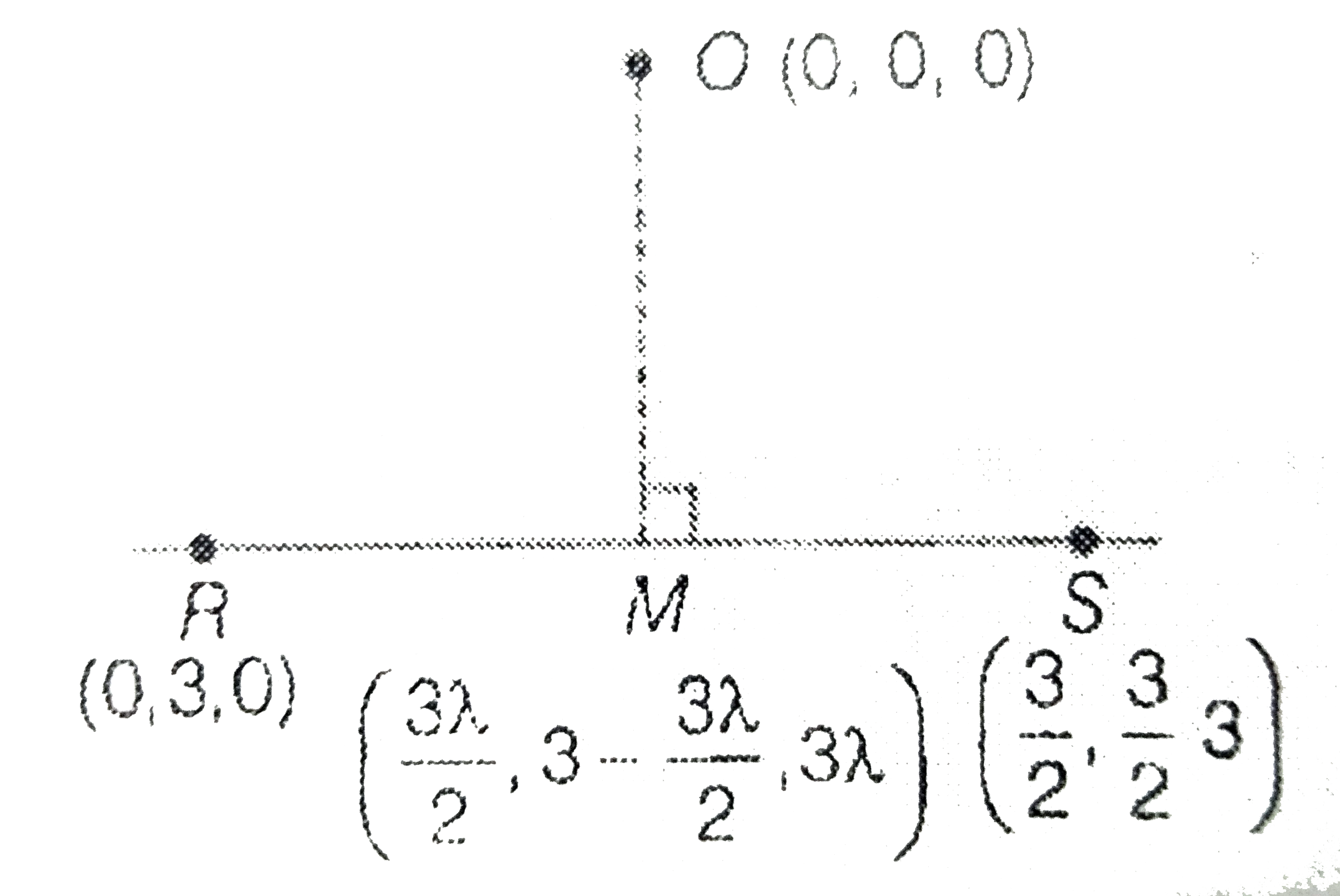
(3λ2,3−3λ2,3λ)(32,323)
∵ ¯¯¯¯¯¯¯OM⊥¯¯¯¯¯RS⇒¯¯¯¯¯¯¯OM.¯¯¯¯¯RS=0
⇒ 9λ4−32(3−3λ2)+3(3λ)=0⇒λ=13
∴M(12,52,1)⇒OM=√14+254+1=√304=√152
∴ Option (d) is correct.
Similar Questions
विचार कीजिये, एक सूच्याकार (pyramid, OPQRS) जो प्रथम अष्टांशक (first octant) (x≥0,y≥0,z≥0) में स्थित है, जिसमें O मुलबिन्दु (origin) तथा OP तथा OR क्रमश: x- अक्ष है | इस सूच्याकार का आधार (base) OPQR एक वर्ग (square) है जिसमें OP = 3 है | बिन्दु S कर्ण (diagonal) OQ के मध्यबिन्दु T के ठीक ऊपर इस प्रकार है कि TS=3 है, तब
View Solutionমনে করো, OPQRS একটি পিরামিড যা প্রথম অষ্টাংশে (x≥0,y≥0,z≥0) অবস্থিত, যেখানে O হল মূলবিন্দু এবং OP,OR যথাক্রমে x-অক্ষ, y-অক্ষ বরাবর অবস্থিত। পিরামিডটির ভূমি OPQR একটি বর্গক্ষেত্র যার OP=3। S বিন্দুটি OQ কর্ণের মধ্যবিন্দু T-এর ঠিক ওপরে অবস্থিত, যেখানে TS=3 । তাহলে
View Solutionयदि रेखा OP, x-अक्ष तथा y-अक्ष से क्रमश: 45° तथा 60∘ का कोण बनाए तथा OP= 12 इकाई है। जहाँ, 0 मूलबिन्दु है, तो P के निर्देशांक हैं
View SolutionIf a line OP through the origin O makes angles α,45∘and60∘ with x, y and z axis respectively then the direction cosines of OP are.
View Solutionविचार कीजिये, एक सूच्याकार (pyramid, OPQRS) जो प्रथम अष्टांशक (first octant) (x≥0,y≥0,z≥0) में स्थित है, जिसमें O मुलबिन्दु (origin) तथा OP तथा OR क्रमश: x- अक्ष है | इस सूच्याकार का आधार (base) OPQR एक वर्ग (square) है जिसमें OP = 3 है | बिन्दु S कर्ण (diagonal) OQ के मध्यबिन्दु T के ठीक ऊपर इस प्रकार है कि TS=3 है, तब
View SolutionConsider a pyramid OPQRS located in the first octan (x≥0,y≥0z≥0) with O as origin, and OP and OR along the x-axis and the y-axis, respectively. The base OPQR of the pyramid is a square with OP =3. The point S is directly above the midpoint T of diagonal OQ such that TS = 3. Then
View SolutionConsider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
View SolutionConsider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin, and OP and OR along the x-axis and the y-axis,respectively. The base OPQR of the pyramid is asqu are with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3.Then
View Solution