If the distance of the point P(1,−2,1) from the plane x+2y−2z=α,whereα>0,is5, then the foot of the perpendicular from P to the place is a. (83,43,−73) b. (43,−43,13) c. (13,23,103) d. (23,−13,−53)Solution in Tamil
(83,43,−73)
(43,43,13)
(13,23,103)
(23,13,52)
The correct Answer is:A
Distance of point P from plane =5
∴ 5=∣∣∣1−4−2−α3∣∣∣
⇒ α=10
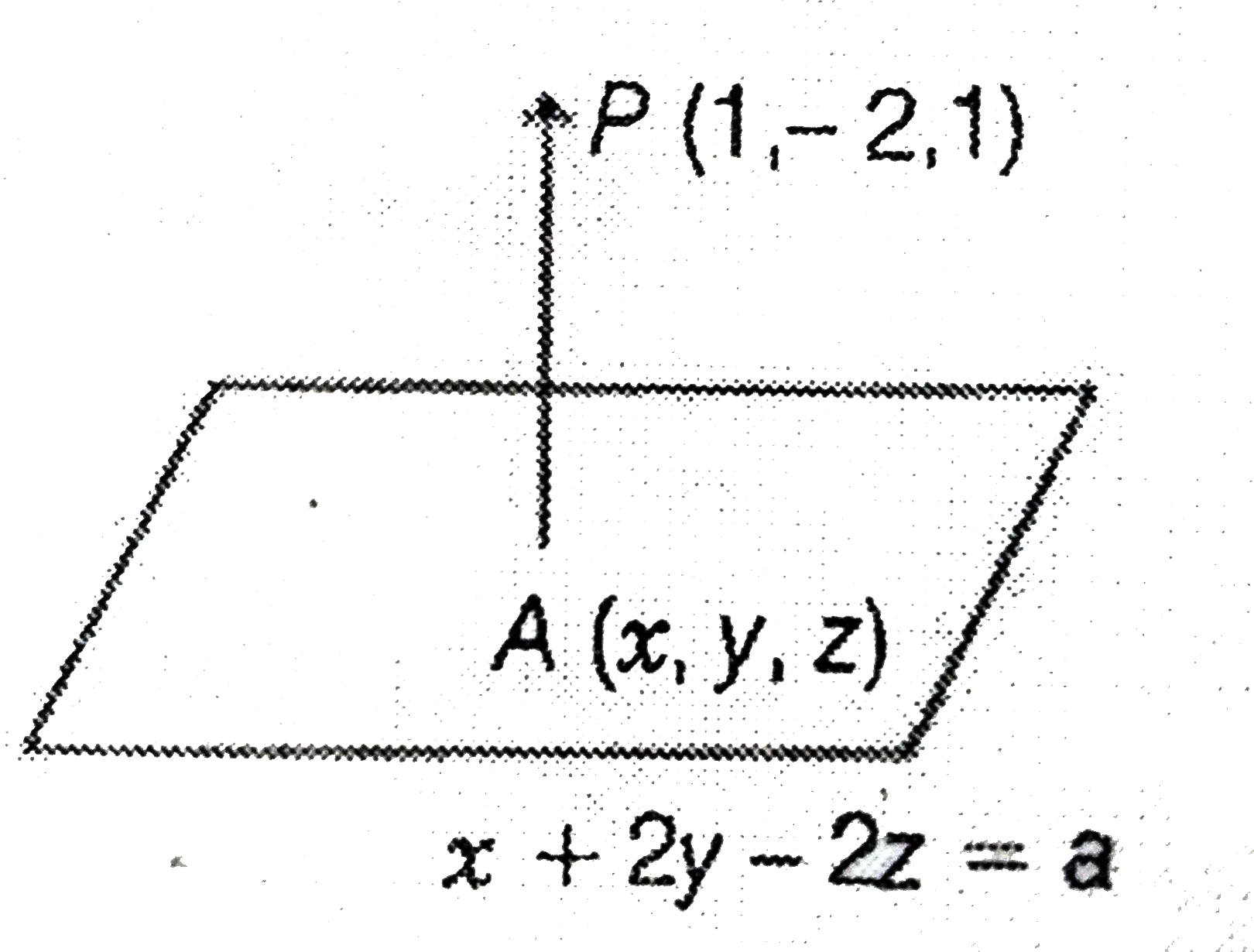
Foot of perpendicular
x−11=y+22=z−1−2=53
⇒ x=83,y=43,z=−73
Thus, the foot of the perpendicular is A(83,43,−73).
Similar Questions
If x+2 is a factor of x2+ax+2b and a+b=4, then (a) a=1, b=3 (b) a=3, b=1 (c) a=−1, b=5 (d) a=5, b=−1
View SolutionThe distance of the point P(4, 3) from the origin is (a) 4 (b) 3 (c) 5 (d) 7
View SolutionFind the distance from the point P(3,2,−1) to the plane containing the points (3,2,−1),(−3,8,−5),(3,2,−5).
View SolutionIf the distance of the point P(1,-2,1) from the plane x+2y-2z=alpha , where alpha>0 , is 5, then the foot of the perpendicular from P to the place is
View SolutionLet A(1, 1, 1), B(3, 7, 4) and C (-1, 3, 0) be three
points in a plane.
The perpendicular distance from C to AB is
View SolutionThe coordinates of the foot of the perpendicular from the point (1,−2,1) on the plane containing the lines, x+16=y−17=z−38andx−13=y−25=z−37, is :
View SolutionIf P(2,3,1) is a point L≡x−y−z−2=0 is a plane then
(A) origin and P lie on the same side of the plane
(B) distance of P from the plane is 4√<br>(3)
(C) foot of perpendicular from point P to plane is(103,53,−13)
(D) image of point P i the planee is (103,53,−13)
View SolutionIf the distance of the point P(1,−2,1) from the plane x+2y−2z=α,whereα>0,is5, then the foot of the perpendicular from P to the place is a. (83,43,−73) b. (43,−43,13) c. (13,23,103) d. (23,−13,−53)
View Solution
