Two lines L1x=5,y3−α=z−2andL2:x=αy−1=z2−α are coplanar. Then α can take value (s) a. 1 b. 2 c. 3 d. 4Solution in Tamil
1
2
3
4
The correct Answer is:A, D
If two straight lines are coplanar,
i.e. x−x1a1=y−y1b1=z−z1c1
and x−x2a2=y−y2b2=z−z2c2 are coplanar
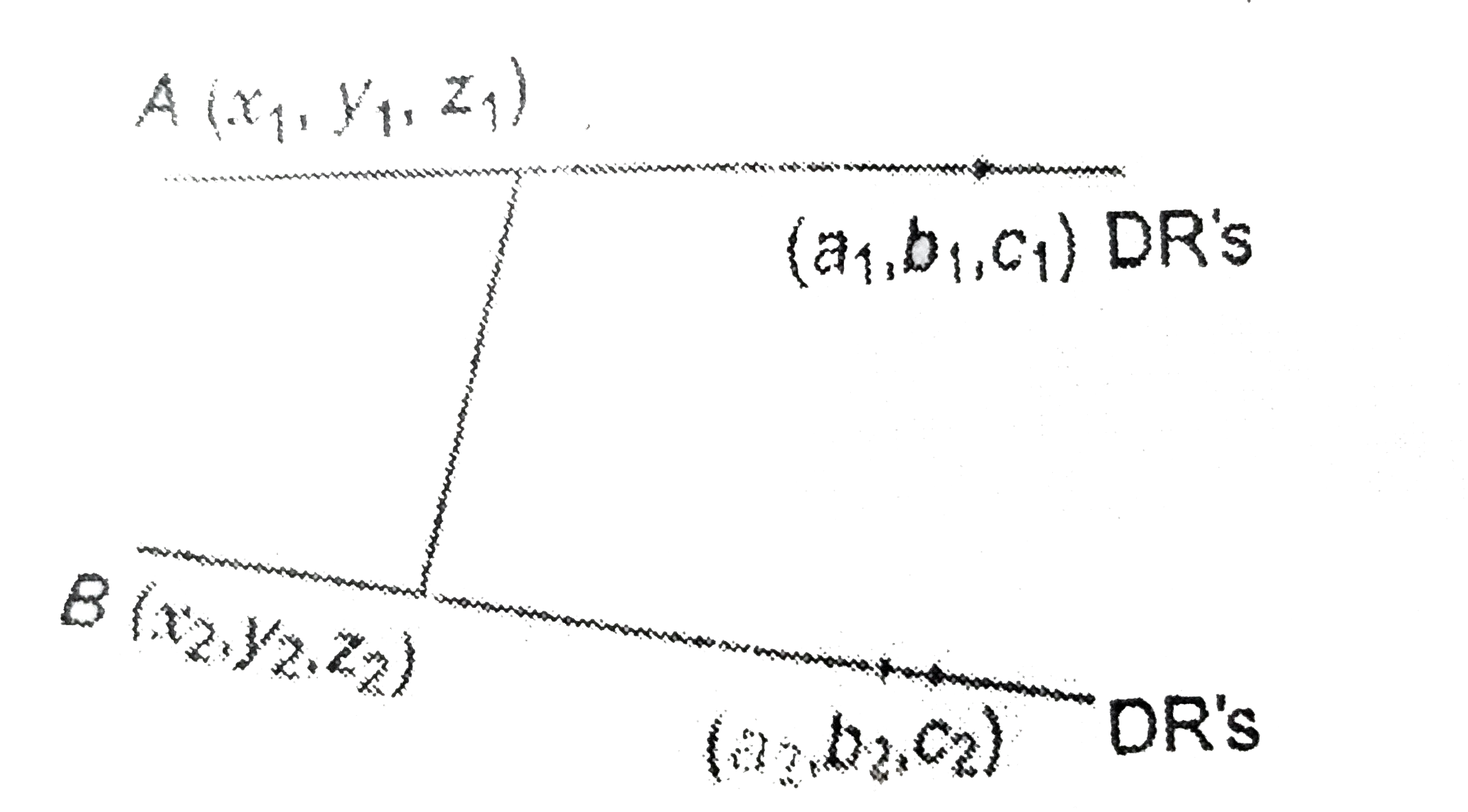
Then, (x2−x1,y2−y1,z2−z1),(a1,b1,c1) and (a2,b2,c2) are coplanar.
i.e. ∣∣
∣
∣∣x2−x1y2−y1z2−z1a1b1c1a2b2c2∣∣
∣
∣∣=0
Here, x=5,y3−α=z−2
⇒ x−50=y−0−(α−3)=z−0−2 ...(i)
and x−α,y−1=z2−α
⇒ x−α0=y−0−1=z−02−α ...(ii)
⇒ ∣∣
∣∣5−α 0 0 03−α −2 0−12−α∣∣
∣∣=0
⇒ (5−α)[(3−α)(2−α)−2]=0
⇒ (5−α)[a2−5α+4]=0
⇒ (5−α)(α−1)(α−4)=0
∴ α=1,4,5
Similar Questions
दो रेखाएँ L1:x=5,y3−α=z−2 तथा L2:x=α,y−1=z2−α समतलीय हैं, तब α का मान हो सकता है
View SolutionTwo lines L _(1) :x =5 , (y)/(3 - alpha) = (z)/(-2) and L _(2) : x = alpa , (y)/(-1) = (z)/(2- alpha ) are coplanar. Then alpha can take value (s)
View Solutionदो रेखाएँ L1:x=5,y3−α=z−2 तथा L2:x=α,y−1=z2−α समतलीय हैं। तब α का मान हो सकता है-
View SolutionTwo lines L_(1) : x=5, (y)/(3-alpha)=(z)/(-2) and L_(2) : x=alpha, (y)/(-1)=(z)/(2-alpha) are coplanar. Then, alpha can take value(s)
View SolutionThe complete set of values of α for which the lines x−12=y−23=z−34andx−32=y−5α=z−7α+2 are coplanar is
View SolutionTwo lines L_1: x=5, y/(3-alpha)=z/(-2) and L_2: x=alpha, y/(-1)=z/(2-alpha) are coplanar. Then alpha can take value (s) a. 1 b. 2 c. 3 d. 4
View SolutionTwo lines L_(1) : x=5, (y)/(3-alpha)=(z)/(-2) and L_(2) : x=alpha, (y)/(-1)=(z)/(2-alpha) are coplanar. Then, alpha can take value(s)
View SolutionTwo lines L_1: x=5, y/(3-alpha)=z/(-2) and L_2: x=alpha, y/(-1)=z/(2-alpha) are coplanar. Then alpha can take value (s) a. 1 b. 5 c. 3 d. 4
View Solution
