The distance of the point from the straight line through the point and parallel to is Solution in Tamil
6
7
The correct Answer is:D
Let point P whose position vector is and a stright line passing through Q(2, 3, -4) parallel to the vector .
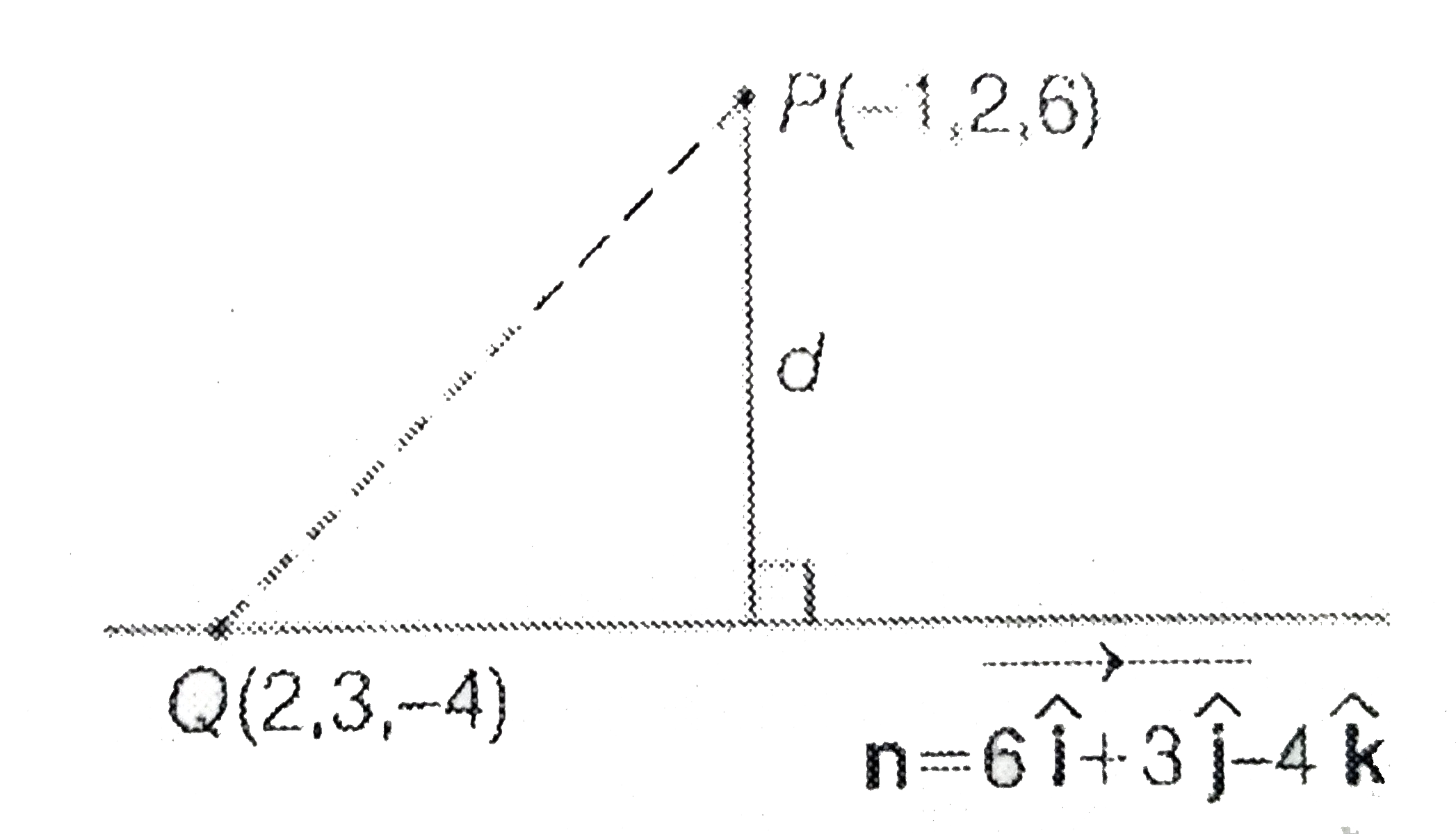
Required distance d=Projection of line segment PQ perpendicular to vector n.
Now, , so
So,
units
Similar Questions
बिंदु (1,2,−4) से गुजरने वाले तथा रेखाओं →r=ˆi+2ˆj−4ˆk+λ(2ˆi+3ˆj+6ˆk) और –r=ˆi−3ˆj+5ˆk+μ(ˆi+ˆj−ˆk) के समांतर समतल के समीकरण के सदिश और कार्तीय रूप ज्ञात कीजिए| साथ ही,इस प्रकार प्राप्त समतल बिंदु (9,−8,−10) की दुरी भी ज्ञात कीजिए|
View SolutionThe equation of plane passing through mid-point of the joining ˆi+2ˆj+4ˆk and −ˆi+2ˆj−6ˆk and perpendicular to it is
View SolutionFind the distance between the lines vecr=hati+2hatj-4hatk+lambda(2hati+3hatj+6hatk) and vecr=3hati+3hatj-5hatk+mu(2hati+3hattj+6hatk) .
View Solutionl1:→r=(ˆi+2ˆj−4ˆk)+λ(2ˆi+3ˆj+6ˆk) এবংl2:→r=(3ˆi+3ˆj−5ˆk)+μ(2ˆi+3ˆj+6ˆk) সরলরেখা দুটির মধ্যে ন্যূনতম দূরত্ব কত?
View SolutionFind the non-parametric form of vector equation, and Cartesian equation vector equation, and Cartesian equation of the plane passing through the point (0, 1,-5) and parallel to the straight lines →r=(ˆi=2ˆj−4ˆk)+s(2ˆi+3ˆj+6ˆk) and →r=(ˆi=3ˆj−4ˆk)+t(ˆi+ˆj+ˆk)
View SolutionLet →OB=ˆi+2ˆj+2ˆk and→OA=4ˆi+2ˆj+2ˆk . The distance of the point B from the straight line passing through A and parallel to the vector 2ˆi+3ˆj+6ˆk is
View SolutionFind the non-parametric form of vector equation, and Cartesian equation vector equation, and Cartesian equation of the plane passing through the point (0, 1,-5) and parallel to the straight lines →r=(ˆi=2ˆj−4ˆk)+s(2ˆi+3ˆj+6ˆk) and →r=(ˆi=3ˆj−4ˆk)+t(ˆi+ˆj+ˆk)
View Solutionमाना −−→OB=ˆi+2ˆj+2ˆk तथा −−→OA∣=4ˆi+2ˆj+2ˆk, बिंदु B की A से गुजरने वाली और सदिश 2ˆi+3ˆj+6ˆk के समान्तर सरल रेखा से दूरी है
View Solution