The position vectors of the vertices, A, B and C of a tetrahedron are $ˆ i + ˆ j + ˆ k, ˆ i and 3 ˆ i$ respectively. The altitude from vertex D to the opposite face ABC meets the median line through A of triangle ABC at a point E. if the length of the side AD is 4 and the volume of the tetrahedron is $2 \sqrt{2} / 3$ find teh position vectors of the point E for all its possible positions . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $- ˆ i + 3 ˆ j + 3 ˆ k and 3 ˆ i - ˆ j - ˆ k$

F is mid- piont of BC i.e., $F = \frac{ˆ i + 3 ˆ i}{2} = 2 ˆ i and A E ⊥ D E$

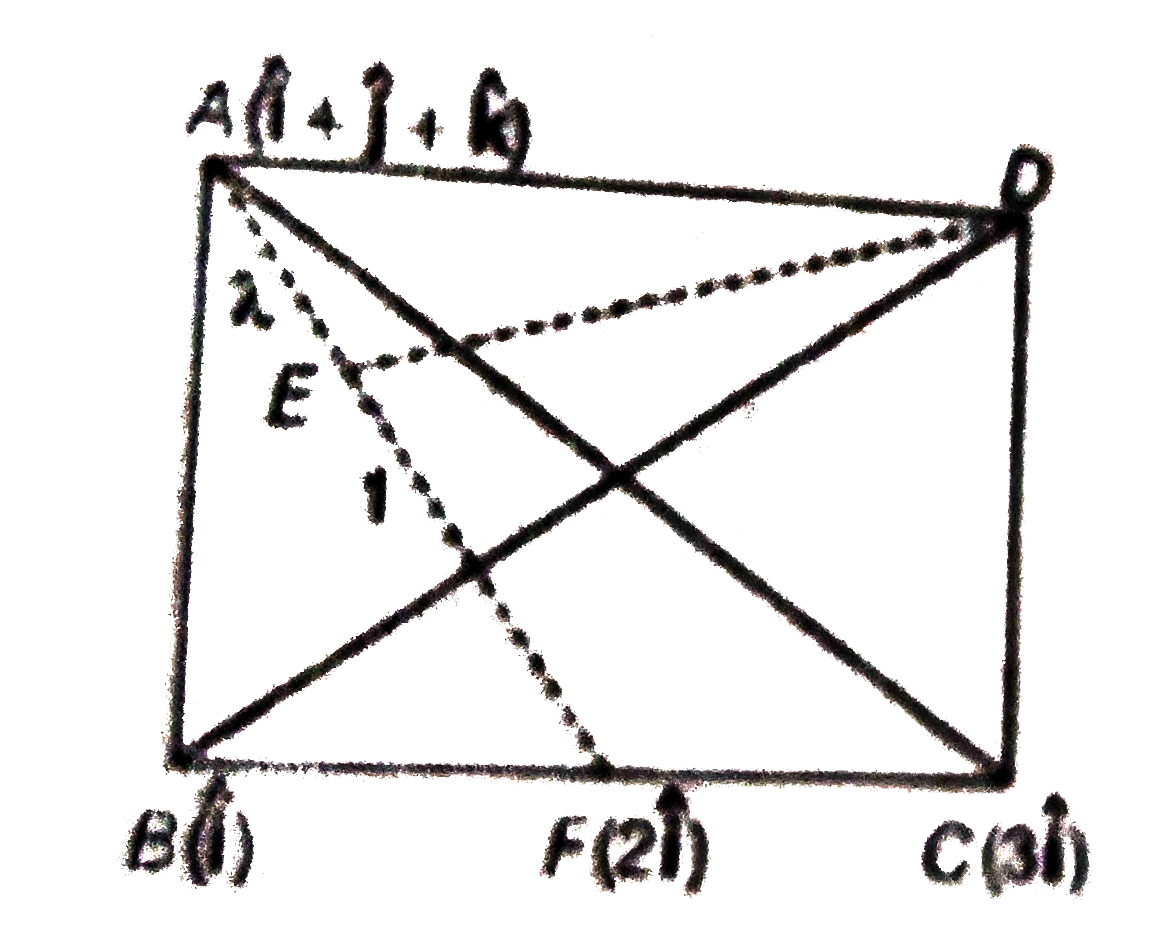
Let E divides AF in $λ : 1$ . The position vectors of E is given by
$(2 λ ˆ i + 1 \frac{ˆ i + ˆ j + ˆ k}{λ + 1} = (\frac{2 λ + 1}{λ + 1}) ˆ i + \frac{1}{λ + 1} ˆ j + \frac{1}{λ + 1} ˆ k$
Now volume of the tetrahedron
$= \frac{1}{3}$ (area of the bases ) (height)
$\Rightarrow \frac{2 \sqrt{2}}{3} = \frac{1}{3} (area of the Δ A B C) (D E)$
But area of the $Δ A B C = \frac{1}{2} ∣ ∣ ∣ - - \to B C \times - - \to B A ∣ ∣ ∣$
$= \frac{1}{2} ∣ ∣ 2 ˆ i \times (ˆ j + ˆ k) ∣ ∣ = ∣ ∣ ˆ i \times ˆ j + ˆ i \times ˆ k ∣ ∣ = ∣ ∣ ˆ k - ˆ j ∣ ∣ = \sqrt{2}$
$∴ \frac{2 \sqrt{2}}{3} = \frac{1}{3} (\sqrt{2}) (D E) \Rightarrow D E = 2$
Since $Δ A D E$ is a right angle triangle then
$\Rightarrow A D^{2} = A E^{2} + D E^{2}$
But $- - \to A E = \frac{2 λ + 1}{λ + 1} ˆ i + \frac{1}{λ + 1} ˆ j + \frac{1}{λ + 1} ˆ k - (ˆ i + ˆ j + ˆ k)$
$= \frac{λ}{λ + 1} ˆ i - \frac{λ}{λ + 1} ˆ j - \frac{λ}{λ + 1} ˆ k$
$\Rightarrow {∣ ∣ ∣ - - \to A E ∣ ∣ ∣}^{2} = \frac{1}{{(λ + 1)}^{2}} [λ^{2} + λ^{2} + λ^{2}] = \frac{3 λ^{2}}{{(λ + 1)}^{2}}$
Theerefore $12 = \frac{3 λ^{2}}{{(λ + 1)}^{2}}$
$\Rightarrow 4 {(λ + 1)}^{2} = λ^{2} \Rightarrow 4 λ^{2} + 4 + δ λ = λ^{2}$
$\Rightarrow 3 λ^{2} + δ λ + 4 = 0 \Rightarrow 3 λ^{2} + 6 λ + 2 λ + 4 = 0$
$\Rightarrow 3 λ (λ + 2) + 2 (λ + 2) = 0$
$\Rightarrow (3 λ + 2) (λ + 2) = 0 \Rightarrow λ - 2 / 3 . λ = - 2$
when $λ = - 2 / 3$ position vectors of E is given by
$(\frac{2 λ + 1}{λ + 1}) ˆ i + \frac{1}{λ + 1} ˆ j + \frac{1}{λ + 1} ˆ k$
$= \frac{2 . (- 2 / 3) + 1}{- 2 / 3 + 1} ˆ i + \frac{1}{- 2 / 3 + 1} ˆ j + \frac{1}{- 2 / 3 + 1} ˆ k$
$= \frac{- 4 / 3 + 1}{\frac{- 2 + 3}{3}} ˆ i + \frac{1}{\frac{- 2 + 3}{3}} ˆ j + \frac{1}{\frac{- 2 + 3}{3}} ˆ k$
$= \frac{\frac{- 4 + 3}{3}}{1 / 3} ˆ i + \frac{1}{1 / 3} ˆ j + \frac{1}{1 / 3} ˆ k = - ˆ i + 3 ˆ j + 3 ˆ k$
and when $λ = - 2,$ position vector of E is given by
$\frac{2 \times (- 2) + 1}{- 2 + 1} ˆ i + \frac{1}{- 2 + 1} ˆ j + \frac{1}{- 2 + 1} ˆ k = \frac{- 4 + 1}{- 1} ˆ i - ˆ j - ˆ k$
$= 3 ˆ i - ˆ j - ˆ k$
Therefore $- ˆ i + 3 ˆ j + 3 ˆ k and + 3 ˆ i - ˆ j - ˆ k$ are the answer.

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile