Let $a = ˆ i + ˆ j + \sqrt{2} ˆ k, b = b_{1} ˆ i + b_{2} ˆ j + \sqrt{2} ˆ k$ and $c = 5 ˆ i + ˆ j + \sqrt{2} ˆ k$ be three vectors such that the projection vector of b on a is a. If $a + b$ is perpendicular to c, then $| b |$ is equal to Solution in Tamil

A

6

B

4

C

$\sqrt{22}$

D

$\sqrt{32}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

According to given information we have the following figure

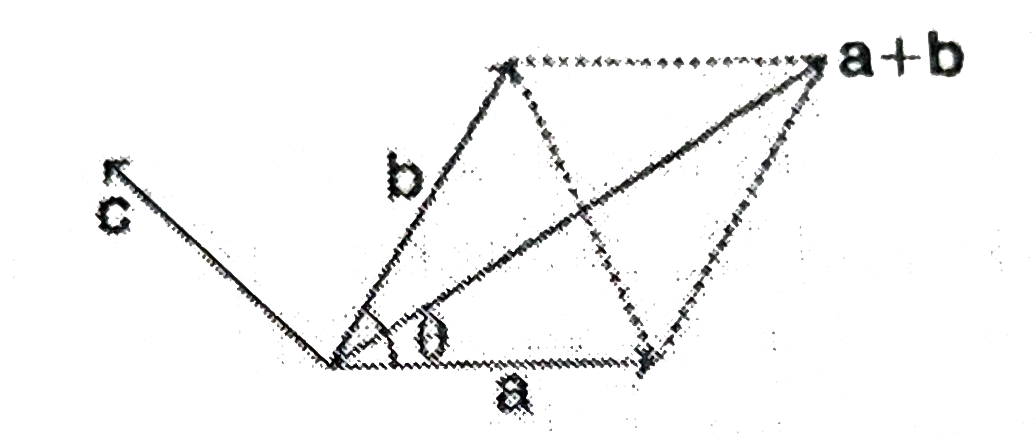
Clearly projection of b on a = $\frac{b . a}{| a |}$
$= \frac{(b_{1} ˆ i + b_{2} ˆ j + \sqrt{2 ˆ k}) (ˆ i + ˆ j + \sqrt{2} ˆ k)}{\sqrt{1^{2} + 1^{2} + {(\sqrt{2})}^{2}}}$
$= \frac{b_{1} + b_{2} + 2}{\sqrt{4}} = \frac{b_{1} + b_{2} + 2}{2}$
but projection of b on a = $| a |$
$∴ \frac{b_{1} + b_{2} + 2}{2} = \sqrt{1^{2} + 1^{2} + {(\sqrt{2})}^{2}}$
$\Rightarrow \frac{b_{1} + b_{2} + 2}{2} = 2 \Rightarrow b_{1} + b_{2} = 2$
Now $a + b = (ˆ i + ˆ j + \sqrt{2} ˆ k) + (b_{1} ˆ i + b_{2} ˆ j +_{\sqrt{2}} ˆ k)$
$= (b_{1} + 1) ˆ i + (b_{2} + 1) ˆ j + 2 \sqrt{2} ˆ k$
$∵ (a + b) ⊥ c$ therefore (a+b) .c =0
$\Rightarrow {(b_{1} + 1) ˆ i + (b_{2} + 1) ˆ j + 2 \sqrt{2} ˆ k} (5 ˆ i + ˆ j + \sqrt{2} ˆ k) = 0$
$\Rightarrow 5 (b_{b_{1} + 1} (b_{2} + 1) + 2 \sqrt{2}) = 0$
$\Rightarrow 5 b_{1} + b_{2} = - 10$
From Eqs (i) and (ii) $b_{1} = - 3$ and $b_{2} = 5$
$\Rightarrow b = - 3 ˆ i + 5 ˆ j + \sqrt{2} ˆ k$
$\Rightarrow | b | = \sqrt{{(- 3)}^{2} + {(5)}^{2} + {(\sqrt{2})}^{2}} = \sqrt{36} = 6$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile