Let f:[0,4π]−−→0,π be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π]satiy∈>he equation f(x)=10−x10 is____Solution in Tamil
The correct Answer is:3
(i) Using definition of f(x)=cos−1(x), we trace the curve f(x)=cos−1(cosx).
(ii) The number of solutions of equations involving tigonometric an algebric functions and involving both functions are found using graphs of the curves.
We know that,cos−1(cosx)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩x,ifx∈[0,π]2π−x,ifx∈[π,2π]−2π+x,if∈[2π,3π]4π−x,ifx∈[3π,4π]
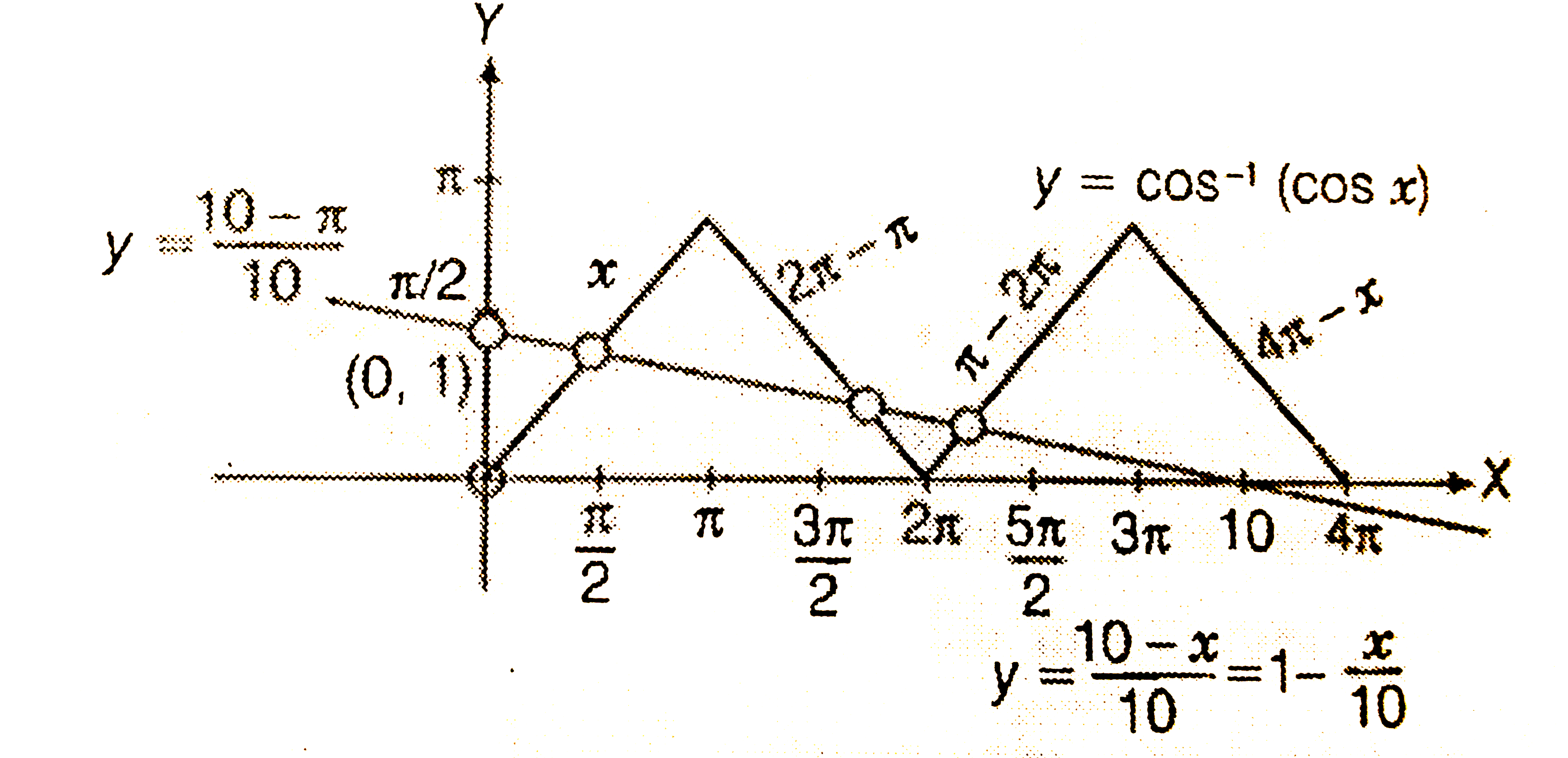
From above graph, it is clear that y=10−x10andy=cos−1(cosx) intersect at three distinct points, so number of solutions is 3.
Similar Questions
Let f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
View SolutionThe number of points of discontinuity for f(x) = sgn(sin x), x∈[0,4π] is ___________.
View SolutionLet f(x)=1−cosxx2, when x≠0, f(x)=1, when x=0 . Show that f(x) is discontinuous at x=0 .
View Solutionagreed f:[0,4pi]to[0,pi],f(x)=cos^(-1)(cosx) Is defined by. Then x epsilon [0,4pi] Equation in f(x)=(10-x)/10 Is the number of points satisfying
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] satisfying the equation f(x)=10−x10 is
View SolutionLetf:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] satisfying the equation f(x)=10−x10 is
View SolutionSupposed that f:[0,4pi] to [0,pi], f(x) = cos^(-1)(cos x) Is defined by. Then [0,4pi] Equation in f(x) = (10-x)/10 Is the number of dots satisfying.
View Solution
