Area of the triangle formed by the line x+y=3
and the angle bisectors of the pairs of straight lines x2−y2+2y=1
is
(a)2squnits
(b)4squnits
(c)6squnits
(d)8squnits
Solution in Tamil
2 sq units
4 sq units
6 sq units
8 sq units
Given, x2−y2+2y=1
⇒x2=(y−1)2
⇒x=y−1 and x=−y+1
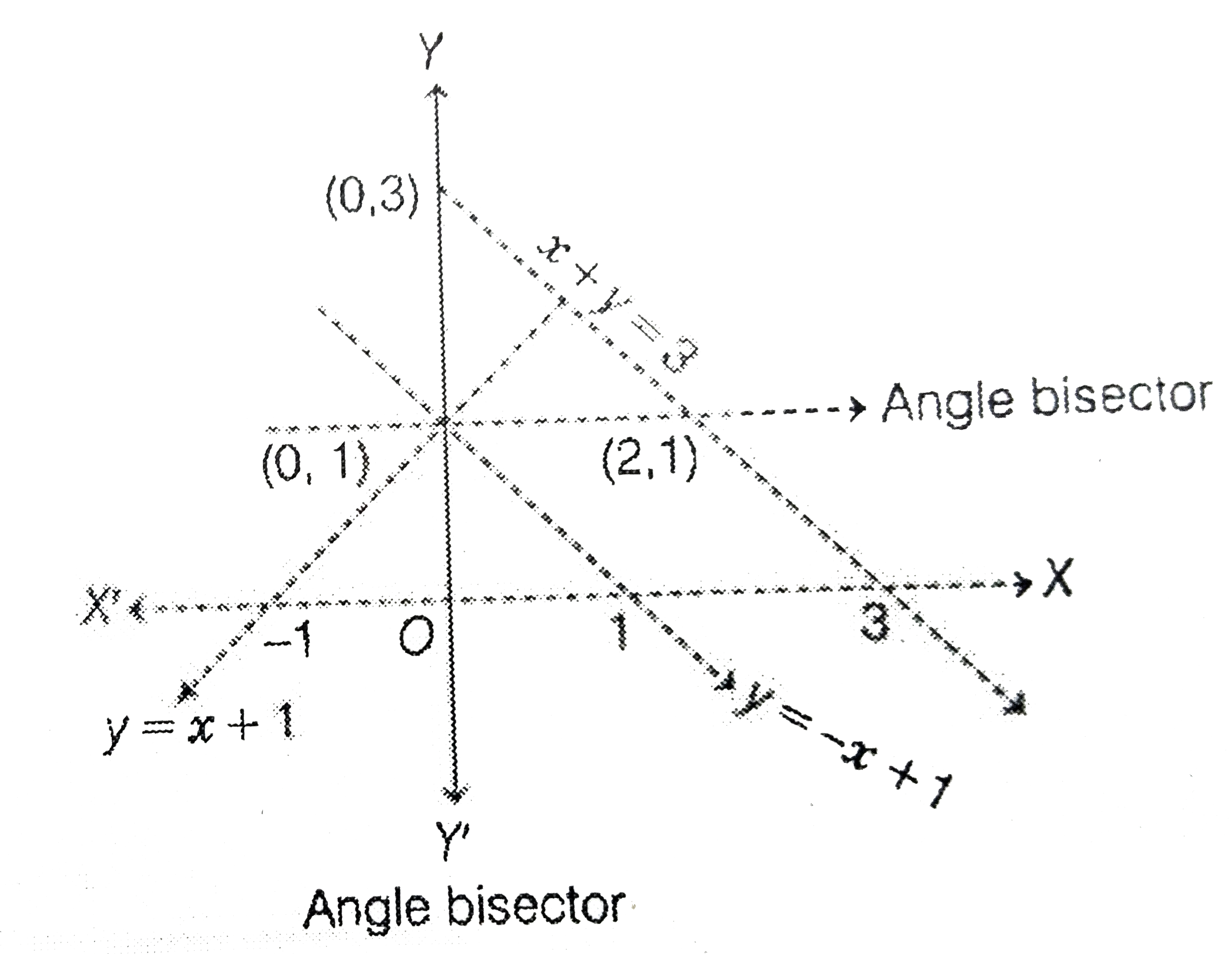
From the graph, it is clear that equation of angle bisectors are
y=1
and x=0
∴ Area of region bounded by x+y=3, x=0
and y=1 is Δ=12×2×2=2sq. units
Similar Questions
If k is the area of the triangle formed by the line x+y=3 and the angle bisectors of the pair of lines x2−y2+2y=1 then k2 is
View SolutionThe area of the region bounded by the lines y=mx,x=1,x=2, and x axis is 6sq. units then 'm' is
View SolutionFind the area of the triangle formed by the line x+y=3 and the angle bisectors of the pair of lines x2−y2+2y=1
View SolutionArea of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is (a) 2 sq units (b) 4 sq units (c) 6 sq units (d) 8 sq units
View SolutionThe area of the triangle formed by the line x=3, y=4 and x=y is (a)12sq.unit (b)1sq.unit (c)2sq.unit (d) None of these
View SolutionThe area of the triangle formed by the straight line x + y = 3 and the angle bisectors of the pair of straight lines x2−y2+2y=1 is
View SolutionThe area (in square units ) of the triangle formed by x+y+1=0 and the pair of straight lines x2−3xy+2y2=0 is :
View SolutionArea of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is
(a)2squnits
(b)4squnits
(c)6squnits
(d)8squnits
View Solution