If a vertex of a triangle is (1, 1) and the mid points of two sides through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle isSolution in Tamil
(1,73)
(13,2)
(13,1)
(13,53)
Let a ΔABC is such that vertices ltbr> A(1,2), B(x1,y1) and C(x2,y2).
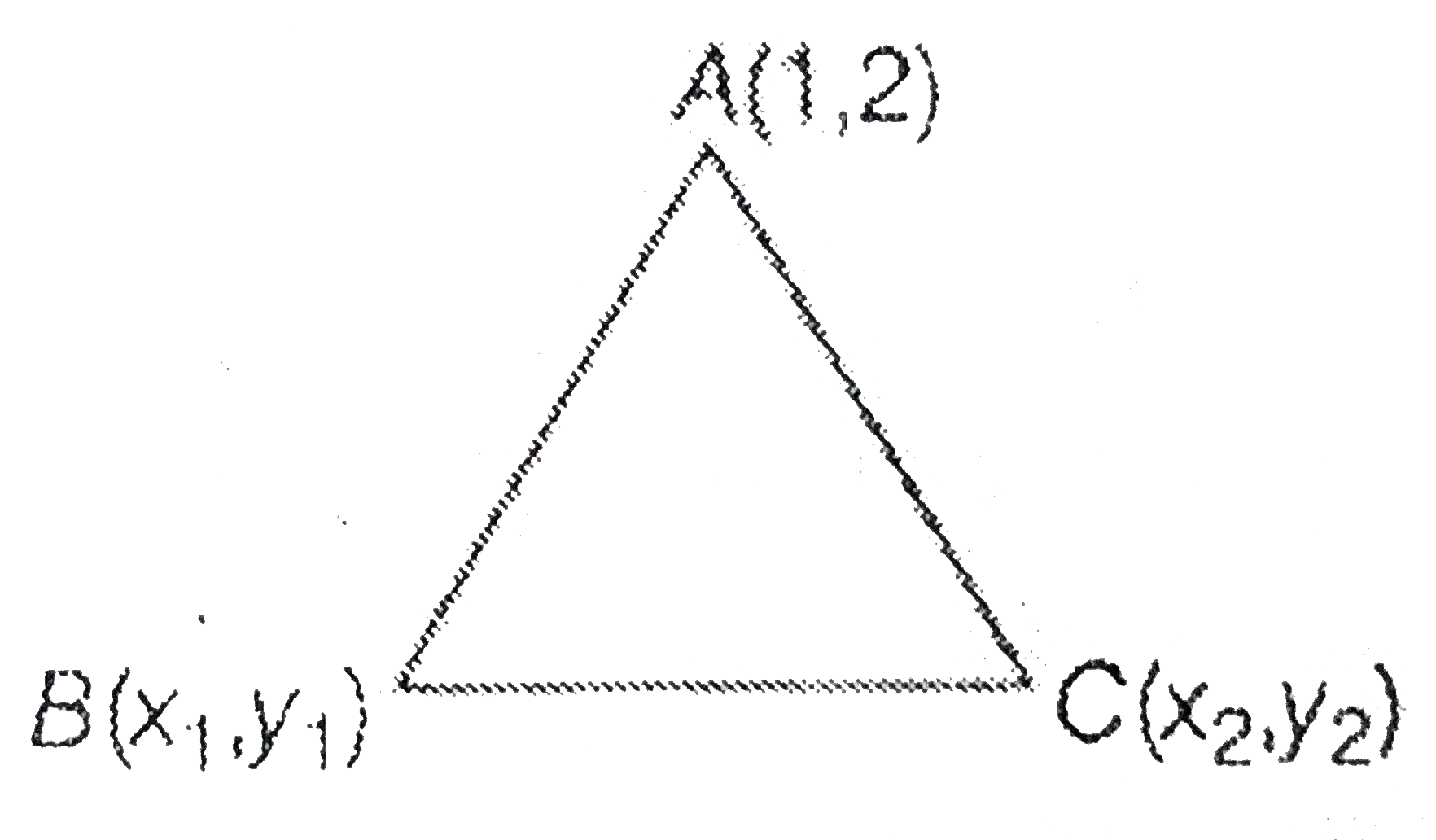
It is given that mid-point of side AB is (−1,1).
So, x1+12=−1
and y1+22=1
⇒x1=−3 and y1=0
So, point B is (−3,0)
Also, it is given that mid-point of side AC is (2,3), so
x2+12=2 and y2+22=3
⇒x2=3 and y2=4
So, point C is (3,4).
Now, centroid of ΔABC is
G(1+(−3)+33,2+0+43)=G(13,2)
Similar Questions
If a vertex of a triangle is (1, 1) and the mid points of two sides through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is
View Solutionएक त्रिभुज का एक शीर्ष (1, 2) पर है तथा इससे होकर जाने वाली दो भुजाओ के मध्य-बिंदु (-1, 1) और (2, 3) हैं, तो इस त्रिभुज का केन्द्रक है
View SolutionIf (32,0),(32,6) and (−1,6) are mid-points of the sides of a triangle, then find
Centroid of the triangle
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionIt the mid-points of the sides of triangle are (1, 2, -3),
(3, 0, 1) and (2, -2, 5), then the centroid is
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionIf (32,0),(32,6) and (−1,6) are mid-points of the sides of a triangle, then find
Centroid of the triangle
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View Solution
