Line $L_{1} \equiv a x + b y + c = 0 and L_{2} \equiv l x + m y + n = 0$ intersect at point P and make an angle $θ$ with each other Find the equation of a line different from $L_{2}$ which passes through P and makes the same angle $θ with L_{1}$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Since, the required line $L$ passes through the intersection of $L_{1} = 0$ and $L_{2} = 0$

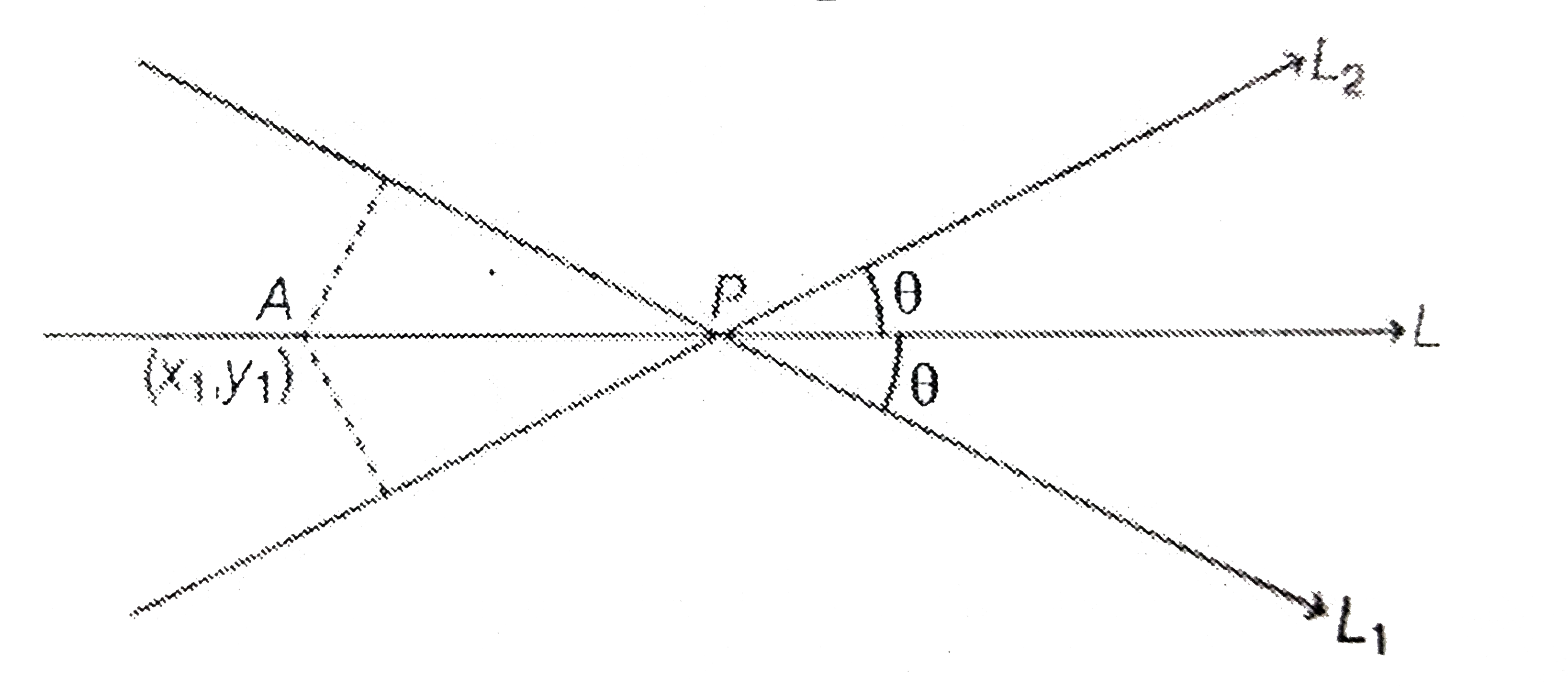
So, the equation of the required line $L$ is
$L_{1} + λ L_{2} = 0$
i.e. $(a x + b y + c) + λ (l x + m y + n) = 0$ …… $(i)$
where, $λ$ is a parameter.
Since, $L_{1}$ is the angle bisector of $L = 0$ and $L_{2} = 0$ .
$∴$ Any point $A (x_{1}, y_{1})$ on $L_{1}$ is equidistant from $L_{1} = 0$ and $L_{2} = 0$
$\Rightarrow \frac{| l x_{1} + m y_{1} + n |}{\sqrt{l^{2} + m^{2}}}$
$= \frac{| (a x_{1} + b y_{1} + c) + λ (l x_{1} + m y_{1} + n) |}{\sqrt{{(a + λ l)}^{2} + {(b + λ m)}^{2}}}$ ....... $(i i)$
But $A (x_{1}, y_{1})$ lies on $L_{1}$ . So, itmust satisfy the equation of $L_{1}$ , ie, $a x_{1} + b y_{1} + c_{1} = 0$
On substituting $a x_{1} + b y_{1} + c = 0$ in Eq. $(i i)$ , we get
$\frac{| l x_{1} + m y_{1} + n |}{\sqrt{l^{2} + m^{2}}} = \frac{| 0 + λ (l x_{1} + m y_{1} + n) |}{\sqrt{{(a + λ l)}^{2} + {(b + λ m)}^{2}}}$
$\Rightarrow λ^{2} (l^{2} + m^{2}) = {(a + λ l)}^{2} + {(b + λ m)}^{2}$
$∴ λ = - \frac{(a^{2}) + b^{2}}{2 (a l + b m)}$
On substituting the value of $λ$ in Eq. $(i)$ , we get
$(a x + b y + c) - (\frac{a^{2} + b^{2}}{2 (a l + b m)} (l x + m y + n) = 0$
$\Rightarrow 2 (a l + b m) (a x + b y + c) - (a^{2} + b^{2}) (l x + m y + n) = 0$
which is the required equation of line $L$ .

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE AND PAIR OF STRAIGHT LINES

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile