Determine all the values of $α$ for which the point $(α, α^{2})$ lies inside the triangle formed by the lines. $2 x + 3 y - 1 = 0$ $x + 2 y - 3 = 0$ $5 x - 6 y - 1 = 0$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Given lines are $2 x + 3 y - 1 = 0$ ……. $(i)$
$x + 2 y - 3 = 0$ …….. $(i i)$
$5 x - 6 y - 1 = 0$ ………. $(i i i)$

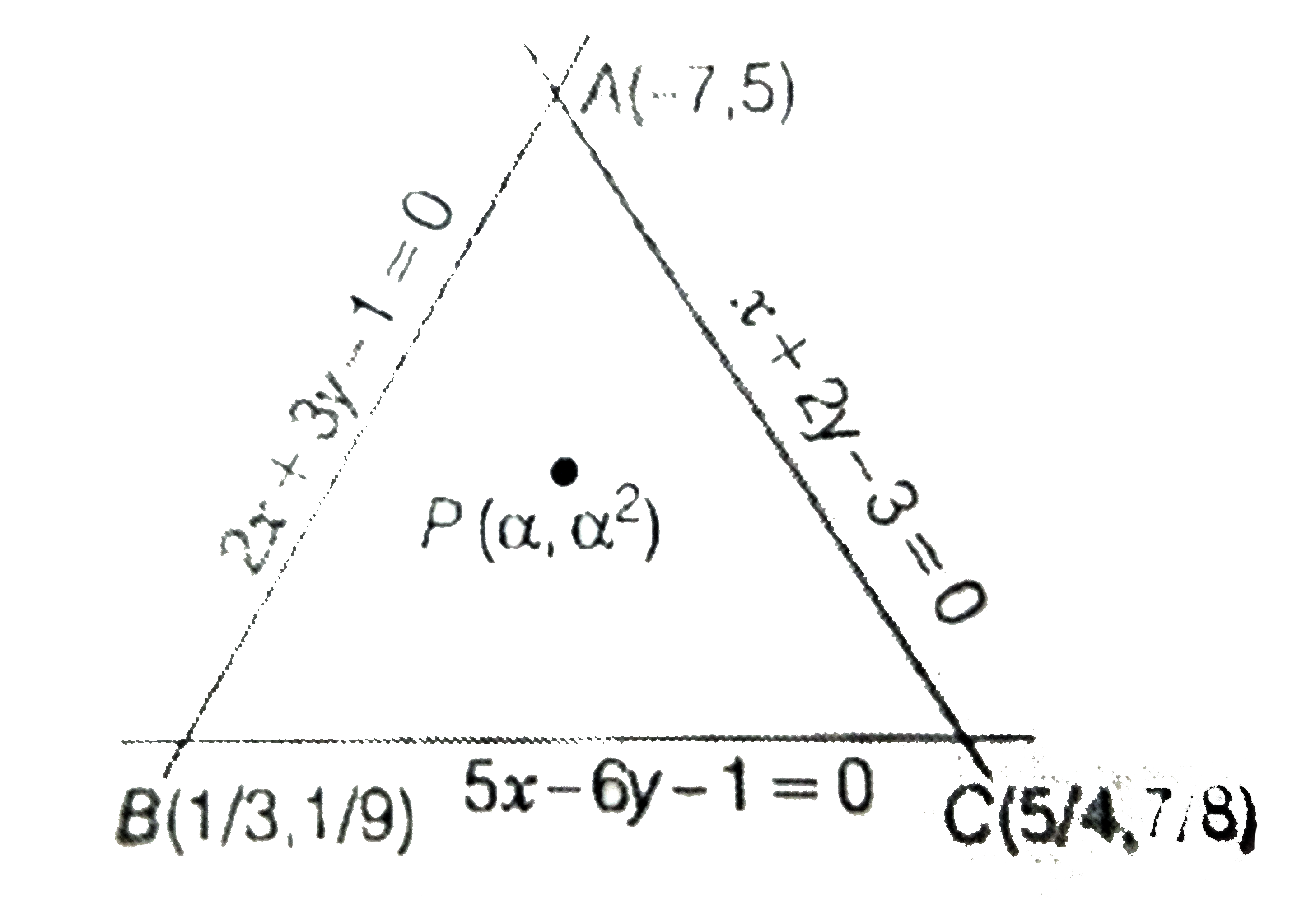
On solving Eqs. $(i), (i i)$ and $(i i i)$ , we get the vertices of a triangle are $A (- 7, 5)$ , $B (\frac{1}{3}, \frac{1}{9})$ and $C (\frac{5}{4}, \frac{7}{8})$ .
Let $P (α, α^{2})$ be a point inside the $Δ A B C$ . Since, $A$ and $P$ are on the same side of $5 x - 6 y - 1 = 0$ , both $5 (- 7) - 6 (5) - 1$ and $5 α - 6 α^{2} - 1$ must have the same sign, therefore
$5 α - 6 α^{2} - 1 < 0$
$\Rightarrow 6 α^{2} - 5 α + 1 > 0$
$\Rightarrow (3 α - 1) (2 α - 1) > 0$
$\Rightarrow α < \frac{1}{3}$ or $α > \frac{1}{2}$ .......... $(i v)$
Also, since $P (α, α^{2})$ and $C (\frac{5}{4}, \frac{7}{8})$ lie on the same side of $2 x + 3 y - 1 = 0$ , therefore both $2 (\frac{5}{4}) + 3 (\frac{7}{8}) - 1$ and $2 α + 3 α^{2} - 1$ must have the same sign.
Therefore, $2 α + 3 α^{2} - 1 > 0$
$\Rightarrow (α + 1) (α - \frac{1}{3}) > 0$
$\Rightarrow α < - 1 \cup α > 1 / 3$ ....... $(v)$
and lastly $(\frac{1}{3}, \frac{1}{9})$ and $P (α, α^{2})$ lie on the same side of the line therefore, $\frac{1}{3} + 2 (\frac{1}{9}) - 3$ and $α + 2 α^{2} - 3$ must have the same sign.
Therefore, $2 α^{2} + α - 3 < 0$
$\Rightarrow 2 α (α - 1) + 3 (α - 1) < 0$
$\Rightarrow (2 α + 3) (α - 1) < 0 \Rightarrow - \frac{2}{3} < α < 1$
On solving Eqs. $(i), (i i)$ and $(i i i)$ , we get the common answer is $- \frac{3}{2} < α < - 1 \cup \frac{1}{2} < α < 1$ .

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE AND PAIR OF STRAIGHT LINES

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile