Question

Let $f:R\to R\text{and}g:R\to R$ be , respectively, given by $f\left(x\right)=\left|x\right|+1\text{and}g\left(x\right)=x^2+1$. Define $h:R\to R$ by $h\left(x\right)=\{\begin{array}{ccc}max.\{f\left(x\right),g\left(x\right)\}\text{,}& & \text{if}x\le 0\\ min.\{f\left(x\right),g\left(x\right)\}\text{,}& & \text{if}x>0\end{array}$
The number of points at which $h\left(x\right)$ is not differentiable is ________.

Answer

3

Explanation

PLAM
(i) In these type of questions, we draw the graph of the function.
(ii) The points at which the curve taken a sharp turn. Are the points of non-differentiability.
Curve of f (x) and g (x) are

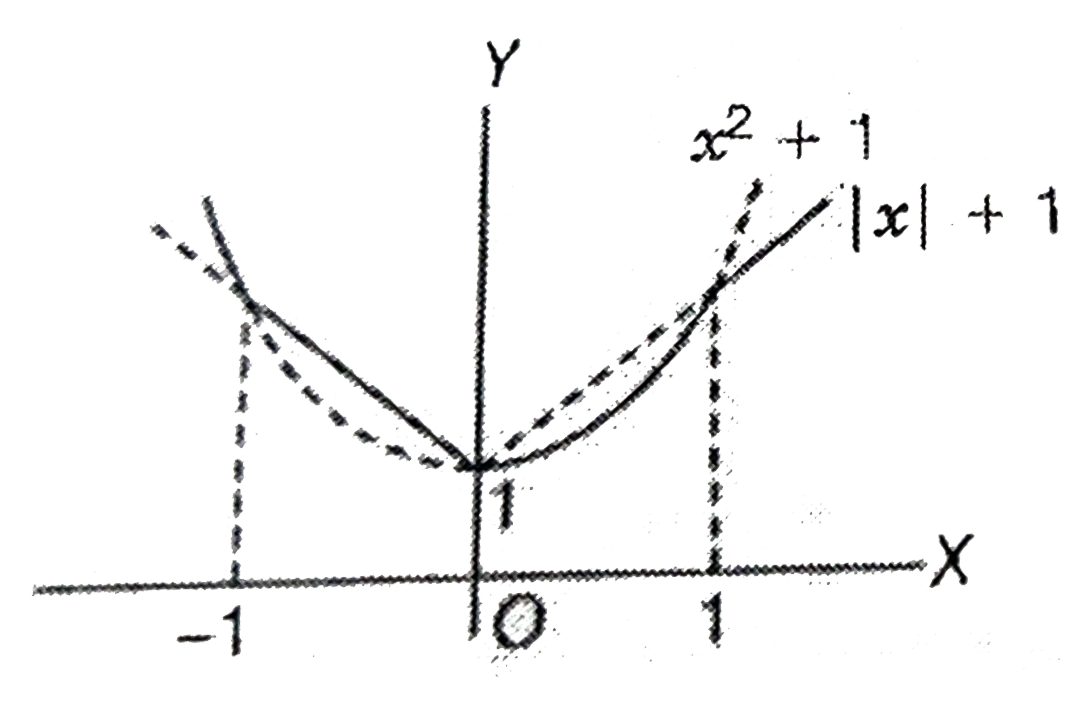
h (x) is not differentiable at `x = pm 1 and 0`.
As, h(x) take sharp turns at ` x = pm 1 and 0`.
Hence, number of points of non-differentiability of h (x) is 3.