Find the area of the region bounded by the x-axis and the curves defined by y=tanx,−π3≤x≤π3 and y=cotx,π6≤x≤3π2Solution in Tamil
Video Solution
Text Solution
The correct Answer is:(12loge3) sq units
Given, y={tanx,−π3≤x≤π3cotx,π6≤x≤π2
which could be plotted as Y-axis.
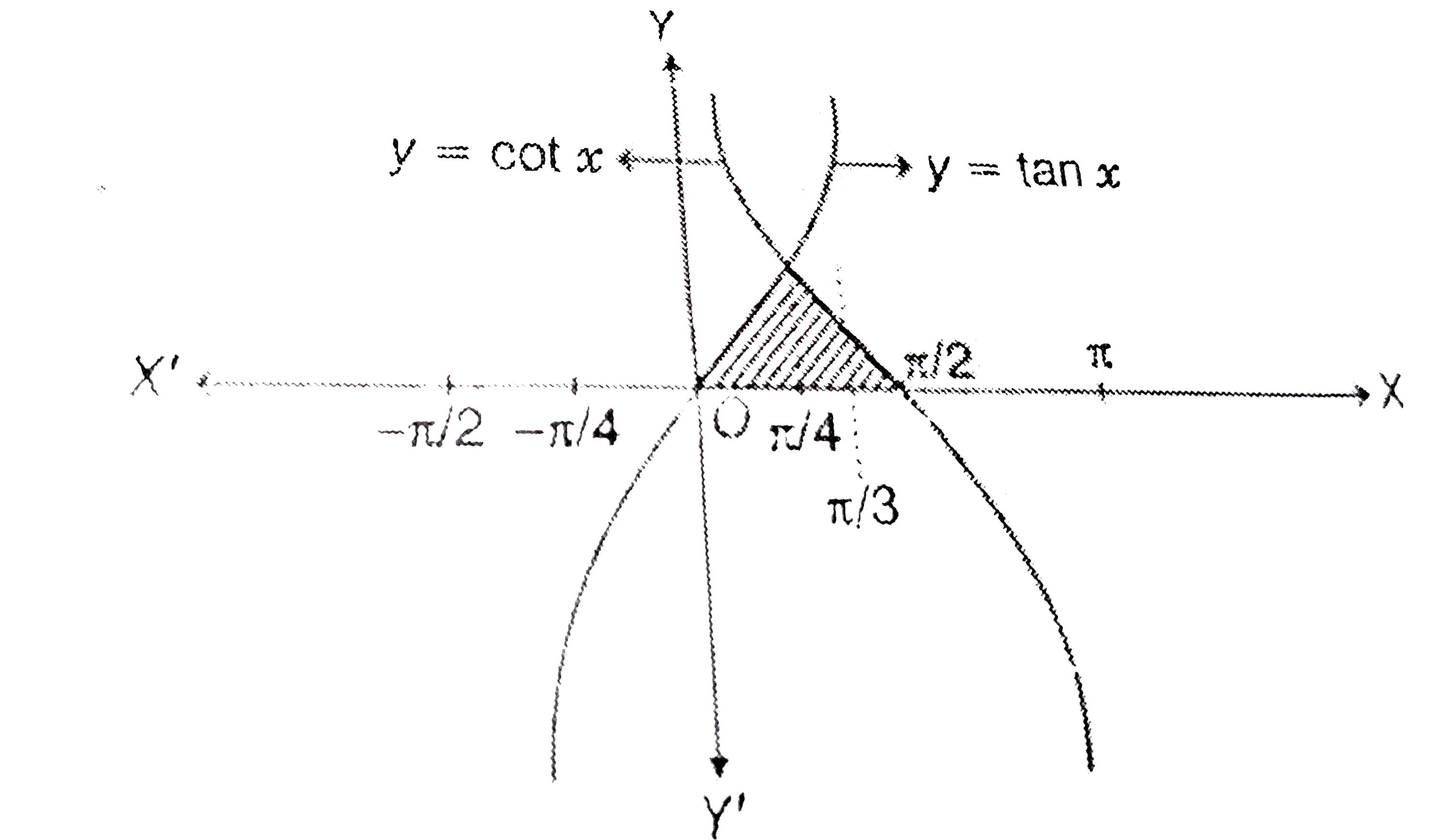
∴Required area =∫π/40(tanx)dx+∫π/3π/4(cotx)dx
=[−log|cosx|]π/40+[logsinx]π/3π/4
=−(log1√2−0)+(log√32−log1√2)
=log√32−2log1√2
=log√32−log12=(12loge3) sq units
|
Similar Questions
The area between the curves y=tanx,y=cotx and X-axis in π6≤x≤π3 is
View SolutionThe area of the region bounded by the x-axis and the curves y=tanx(−π3≤x≤π3) and y=cotx(π6≤x≤3π2) is
View SolutionThe area of the region above x-axis bounded by y=cotx,π12≤x≤π4 is
View SolutionFind the area of the region bounded by the x-axis and the curves defined by y=tanx,
(where −π3≤x≤π3) and y=cotx.(where π6≤x≤2π3)
View SolutionArea of the area bounded by the curve y = tanx and x-axis (where - pi//3 le x le pi//3 ) Will happen
View SolutionArea of the region bounded by the curve y=sinxandx -axis −π2≤x≤π2 ………
View SolutionThe area of the region bounded by the curve y=cosx,−π2≤x≤π2and X - axis is …sq .unit
View SolutionThe area of the region bounded by the X-axis and
the curves defined by y=tanx, (−π3≤x≤π3) is
View Solution
