Question

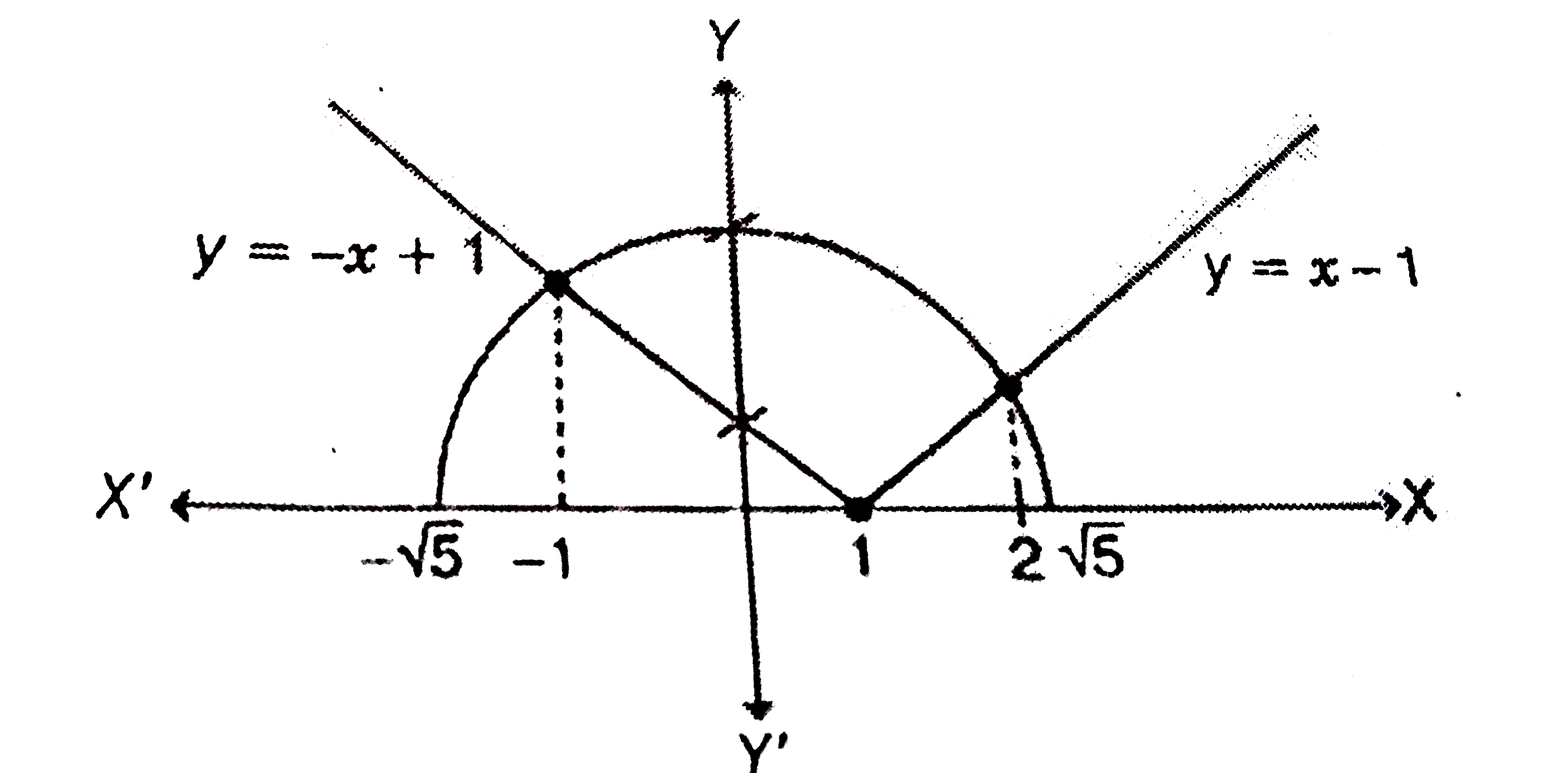
Sketch the region bounded by the curves $y=\sqrt{5-x^2}\text{and}y=|x-1|$ and find its area.

Answer

`((5pi)/(4)-(1)/(2))` sq units

Explanation

Given curves `y=sqrt(5-x^(2)) and y=|x-1|` could be sketched as shown, whose point of intersection are
`5-x^(2)=(x-1)^(2)`

`rArr 5-x^(2) =x^(2)-2x+1`
` 2x^(2) -2x-4=0`
`rArr x =2,-1`
`therefore ` Required area
`=int_(-1)^(2)sqrt(5-x^(2))dx -int_(-1)^(1)(-x+1)dx-int_(-1)^(1)(-x+1)dx -int_(1)^(2)(x-1)dx`
`=[(x)/(2) sqrt(5-x^(2))+(5)/(2) sin^(-1)((x)/(sqrt(5)))]_(-1)^(2)-[(-x^(2))/(2)+x]_(-1)^(1) -[(x^(2))/(2)-x]_(1)^(2)`
`=(1+(5)/(2)"sin"^(-1)(2)/(sqrt(5)))-[-1+(5)/(2)sin^(-1)((-1)/(sqrt(5)))]-(-(1)/(2)+1+(1)/(2)+1)-(2-2-(1)/(2)+1)`
`=(5)/(2)("sin"^(-1)(2)/(sqrt(5))+"sin"^(-1)(1)/(sqrt(5)))-(1)/(2)`
`=(5)/(2) sin^(-1)((2)/(sqrt(5)) sqrt(1-(1)/(5))+(1)/(sqrt(5))sqrt(1-(4)/(5)))-(1)/(2)`
`=(5)/(2) sin^(-1)(1)-(1)/(2)=((5pi)/(4)-(1)/(2))` sq units