Find the area of the region bounded by the curve C:y=tanx,tan≥ntdrawn→C at x=π4, and the x-axis.Solution in Tamil
The correct Answer is:[(log√2−14) sq units ]
Given, y=tanx⇒dydx=sec2x
∴(dydx)x=π4=2
Hence, equation of tangent at A(π4,1) is
y−1x−π/4=2⇒y−1=2x−π2
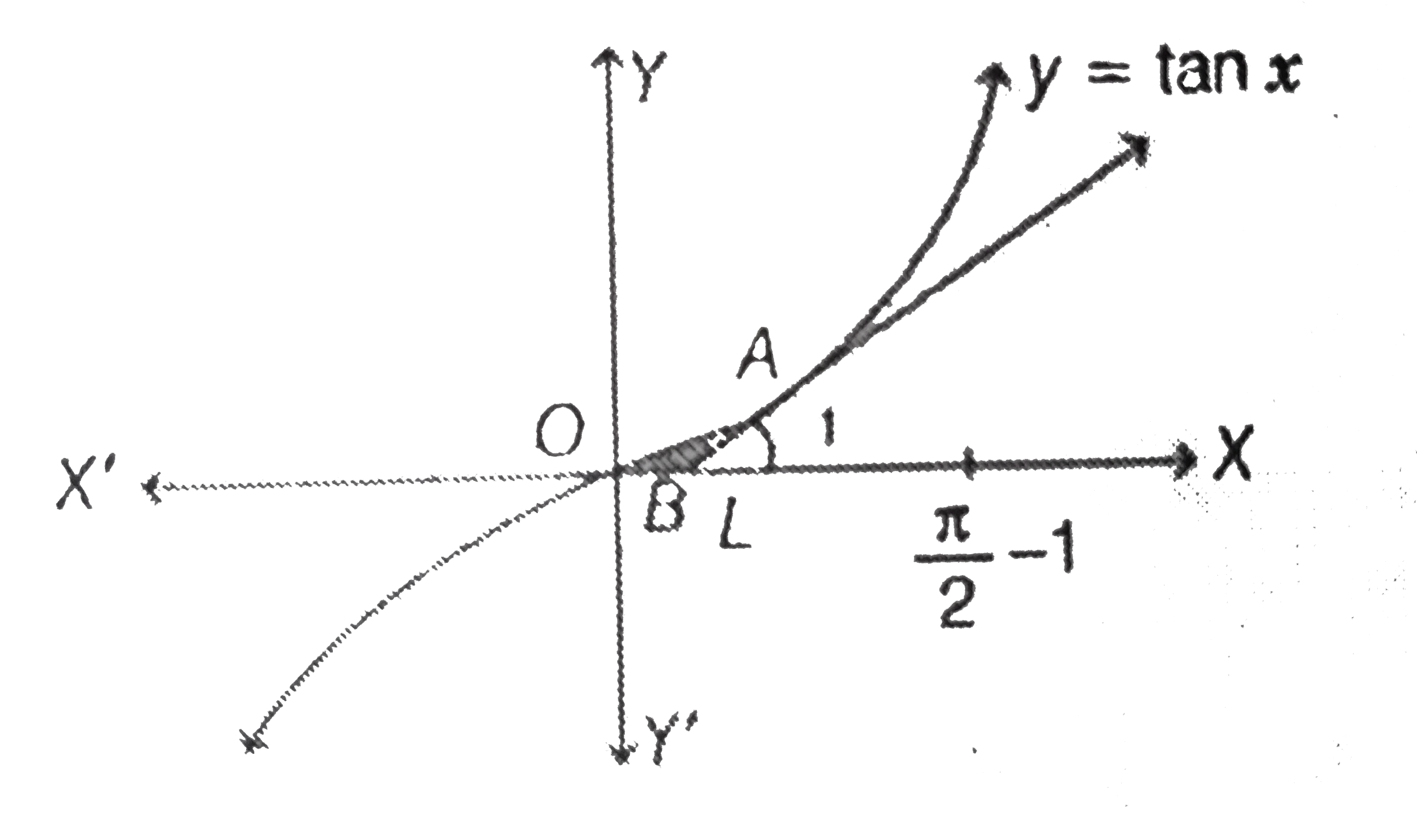
⇒(2x−y)=(π2−1)
∴ Required area is OABO
=∫π/40(tanx)dx−area of ΔALB
=[log|secx|]π/40−12.BL.AL
=log√2−12(π4−π−24)⋅1
=(log√2−14) sq unit
Similar Questions
Area of the region bounded by the x-axis and curves y=tanx(−π/3≤x≤π/3)andy=cotx(π/6≤x≤3π/2) is
View SolutionFind the area of the region bounded by x-axis, the curve y=|cosx|, the lines x=0 and x=π.
View SolutionThe area of the region bounded by the curve y=tanx tangent drawn to the curve at x=π/4 and the x-axis is
View SolutionFind the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.
View SolutionFind the area of the region bounded by the curve C:y=tanx,tan≥ntdrawn→C at x=π4, and the x-axis.
View SolutionFind the area of the region bounded by the curve y = sin x, the X−axis and the given lines x=−π,x=π
View SolutionFind the area of that region bounded by the curve y=cosx, X-axis, x=0 and x=π.
View SolutionFind the area of the region bounded by the curve C:y=tanx,tan≥ntdrawn→C at x=π4, and the x-axis.
View Solution
