For which of the following values of m is the area of the regions bounded by the curve y=x−x2 and the line y=mx equal 92? −4 (b) −2 (c) 2 (d) 4Solution in Tamil
-4
-2
2
4
The correct Answer is:B, D
Case I When m = 0
In this case, y=x−x2 …(i),
and y=0 …(ii)
are two given curves, y>0 is total region above X-axis.
Therefore, area between y=x−x2 and y=0
is area between y=x−x2 and above the X-axis

∴A=∫10(x−x2)dx=[x22−x33]10=12−13=16≠92
Hence, no solutation exists.
Case II When m<0
In this case, area between y=x−x2 and y=mx is OABCO and points of intersection are (0,0) and
{1−m,m(1−m)}.
∴ Area of curve OABCO =∫1−m0[x−x2−mx]dx

=[(1−m)x22−x33]1−m0
=12(1−m)3−13(1−m)3=16(1−m)3
∴16(1−m)3=92 [given]
⇒(1−m)3=27
⇒1−m=3
⇒m=−2
Case III When m>0
In this case, y=mx and y=x−x2 intersect in (0,0) and
{(1−m),m(1−m)} as shown in figure
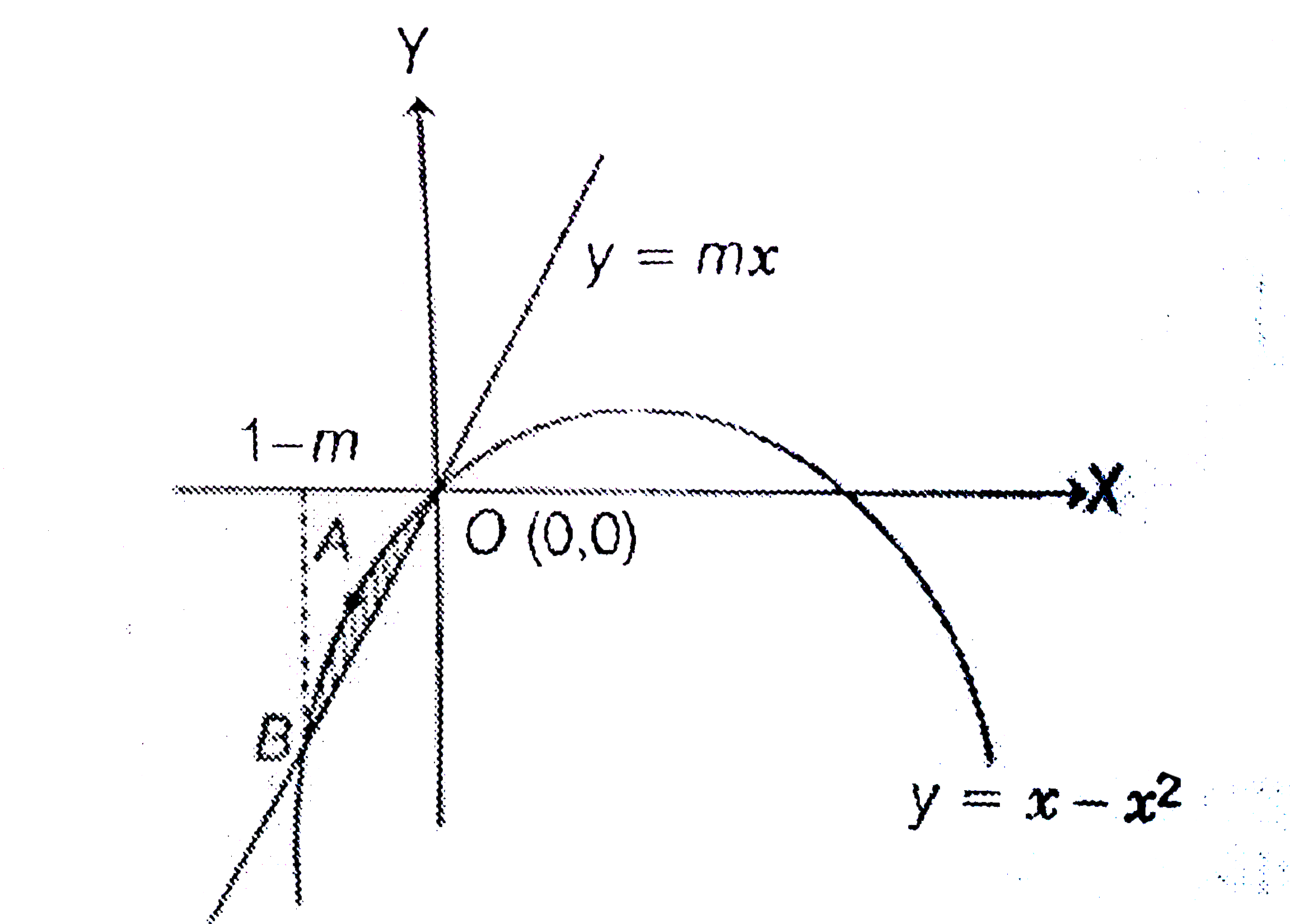
∴ Area of shaded region =∫01−m(x−x2−mx)dx
=[(1−m)x22−x33]01−m
=−12(1−m)(1−m)2+13(1−m)3
=−16(1−m)3
⇒92=−16(1−m)3 [given]
⇒(1−m)3=−27
⇒(1−m)=−3
⇒m=3+1=4
Therefore, (b) and (d) are the answers.
Similar Questions
For which of the following values of m, is the area of the region bounded by the curve y=x−x2 and the line y = mx equals 92 ?
View SolutionFor which of the following values of m is the area of the regions bounded by the curve y=x−x2 and the line y=mx equal 92? (a) −4 (b) −2 (c) 2 (d) 4
View SolutionWhich values of m for the following y=x-x^2 And the area bounded by the line y = mx is equal to 9/2.
View SolutionThe area of region bounded by the curve y=x−x2 and line y=mx is 92 then the value of m is ……..
View Solutionनिम्नलिखित में से m के किस मान के लिए वक्र y=x−x2 तथा रेखा y=mx के द्वारा परिबद्ध क्षेत्र का क्षेत्रफल 9/2 के बराबर है
View SolutionThe area of the region bounded by the curve y=x2 and y = x is equal to
View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View SolutionFind the area of the region bounded by the curves x2+y2=4 and (x−2)2+y2=4.
View Solution
